Вопрос 1. Что такое вектор? Как обозначаются векторы?
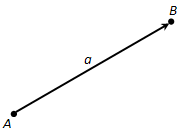
Ответ. Вектором мы будем называть направленный отрезок (рис. 211). Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами a, b, c, ... . Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова "вектор" над буквенным обозначением вектора иногда ставится стрелка или черта. Вектор на рисунке 211 можно обозначить так:

\(\overline{a}\), \(\overrightarrow{a}\) или \(\overline{AB}\), \(\overrightarrow{AB}\).

Вопрос 2. Какие векторы называются одинаково направленными (противоположно направленными)?
Ответ. Векторы \(\overline{AB}\) и \(\overline{CD}\) называются одинаково направленными, если полупрямые AB и CD одинаково направлены.
Векторы \(\overline{AB}\) и \(\overline{CD}\) называются противоположно направленными, если полупрямые AB и CD противоположно направлены.
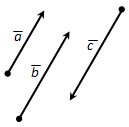
На рисунке 212 векторы \(\overline{a}\) и \(\overline{b}\) одинаково направлены, а векторы \(\overline{a}\) и \(\overline{c}\) противоположно направлены.

Вопрос 3. Что такое абсолютная величина вектора?
Ответ. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора \(\overline{a}\) обозначается |\(\overline{a}\)|.

Вопрос 4. Что такое нулевой вектор?
Ответ. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (\(\overline{0}\)). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.

Вопрос 5. Какие векторы называются равными?
Ответ. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.

Вопрос 6. Докажите, что равные векторы одинаково направлены и равны по абсолютной величине. И обратно: одинаково направленные векторы, равные по абсолютной величине, равны.
Ответ. При параллельном переносе вектор сохраняет своё направление, а также свою абсолютную величину. Значит, равные векторы направлены одинаково и равны по абсолютной величине.
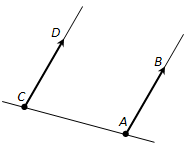
Пусть \(\overline{AB}\) и \(\overline{CD}\) – одинаково направленные векторы, равные по абсолютной величине (рис. 213). Параллельный перенос, переводящий точку C в точку A, совмещает полупрямую CD с полупрямой AB, так как они одинаково направлены. А так как отрезки AB и CD равны, то при этом точка D совмещается с точкой B, т.е. параллельный перенос переводит вектор \(\overline{CD}\) в вектор \(\overline{AB}\). Значит, векторы \(\overline{AB}\) и \(\overline{CD}\) равны, что и требовалось доказать.

Вопрос 7. Докажите, что от любой точки можно отложить вектор, равный данному вектору, и только один.
Ответ. Пусть CD – прямая, а вектор \(\overline{CD}\) – часть прямой CD. Пусть AB – прямая, в которую переходит прямая CD при параллельном переносе, \(\overline{AB}\) – вектор, в который при параллельном переносе переходит вектор \(\overline{CD}\), а значит, векторы \(\overline{AB}\) и \(\overline{CD}\) равны, а прямые AB и CD параллельны (см. рис. 213). Как мы знаем, через точку не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной (аксиома параллельных прямых). Значит, через точку A можно провести одну прямую, параллельную прямой CD. Так как вектор \(\overline{AB}\) – часть прямой AB, то через точку A можно провести один вектор \(\overline{AB}\), равный вектору \(\overline{CD}\).

Вопрос 8. Что такое координаты вектора? Чему равна абсолютная величина вектора с координатами a₁, a₂?
Ответ. Пусть вектор \(\overline{a}\) имеет началом точку A₁ (x₁; y₁), а концом точку A₂ (x₂; y₂). Координатами вектора \(\overline{a}\) будем называть числа a₁ = x₂ - x₁, a₂ = y₂ - y₁. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае \(\overline{a}\) (a₁; a₂) или просто \((\overline{a₁; a₂})\). Координаты нулевого вектора равны нулю.
Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a₁, a₂ равна \(\sqrt{a^2₁ + a^2₂}\).

Вопрос 9. Докажите, что равные векторы имеют соответственно равные координаты, а векторы с соответственно равными координатами равны.
Ответ. Пусть A₁ (x₁; y₁) и A₂ (x₂; y₂) – начало и конец вектора \(\overline{a}\). Так как равный ему вектор \(\overline{a'}\) получается из вектора \(\overline{a}\) параллельным переносом, то его началом и концом будут соответственно A'₁ (x₁ + c; y₁ + d), A'₂ (x₂ + c; y₂ + d). Отсюда видно, что оба вектора \(\overline{a}\) и \(\overline{a'}\) имеют одни и те же координаты: x₂ - x₁, y₂ - y₁.
Докажем теперь обратное утверждение. Пусть соответствующие координаты векторов \(\overline{A₁A₂}\) и \(\overline{A'₁A'₂}\) равны. Докажем, что векторы равны.
Пусть x'₁ и y'₁ - координаты точки A'₁, а x'₂, y'₂ - координаты точки A'₂. По условию теоремы x₂ - x₁ = x'₂ - x'₁, y₂ - y₁ = y'₂ - y'₁. Отсюда x'₂ = x₂ + x'₁ - x₁, y'₂ = y₂ + y'₁ - y₁. Параллельный перенос, заданный формулами

x' = x + x'₁ - x₁, y' = y + y'₁ - y₁,

переводит точку A₁ в точку A'₁, а точку A₂ в точку A'₂, т.е. векторы \(\overline{A₁A₂}\) и \(\overline{A'₁A'₂}\) равны, что и требовалось доказать.

Вопрос 10. Дайте определение суммы векторов.
Ответ. Суммой векторов \(\overline{a}\) и \(\overline{b}\) с координатами a₁, a₂ и b₁, b₂ называется вектор \(\overline{c}\) с координатами a₁ + b₁, a₂ + b a₂, т.е.

\(\overline{a} (a₁; a₂) + \overline{b}(b₁; b₂) = \overline{c} (a₁ + b₁; a₂ + b₂)\).