Мавод дар асоси китоби «Геометрия»-и математик А.В. Погорелов тартиб дода шудааст.
Саволи 1. Ду хати росте, ки ба хати рости сеюм параллел аст, ба якдигар параллел мебошанд. Инро исбот кунед.
Ҷавоб. Теоремаи 4.1. Ду хати росте, ки ба хати рости сеюм параллел аст, ба якдигар параллел мебошанд.
Исбот.Бигзор хатҳои рости a ва b ба хати рости c параллел бошанд. Фарз мекунем, ки хатҳои a ва b параллел нестанд (расми 69).
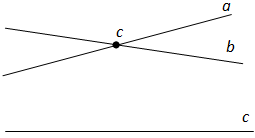
Расми 69
Он гоҳ онҳо дар ягон нуқтаи C якдигарро мебуранд. Пас, ду хати росте, ки ба хати рости c параллел мебошанд, аз нуқтаи C мегузаранд. Лекин ин ғайри имкон аст, чунки аз нуқтае, ки дар хати рости додашуда воқеъ нест, фақат як хати росте гузаронидан мумкин аст, ки ба хати рости додашуда параллел аст. Теорема исбот шуд.
Саволи 2. Чӣ гуна кунҷҳо кунҷҳои дарунии яктарафа номида мешаванд? Чӣ гуна кунҷҳо кунҷҳои дарунии чилликӣ номида мешаванд? Шарҳ диҳед.
Ҷавоб. Кунҷҳое, ки дар натиҷаи хатҳои рости AB ва CD-ро буридани AC ҳосил мешаванд, номи махсус доранд.
Агар нуқтаҳои B ва D нисбат ба хати рости AC дар як нимҳамворӣ бошанд, онгоҳ кунҷҳои BAC ва DCA-ро кунҷҳои дарунии яктарафа меноманд (расми 71, а).
Агар нуқтаҳои B ва D нисбат ба хати рости AC дар нимҳамвориҳои гуногун бошанд, онгоҳ кунҷҳои BAC ва DCA-ро кунҷҳои дарунии чилликӣ меноманд (расми 71, б).
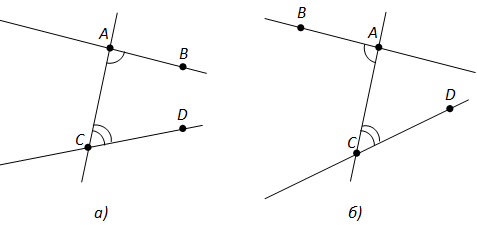
Расми 71
Саволи 3. Агар кунҷҳои дарунии чилликии як ҷуфт кунҷҳо баробар бошанд, он гоҳ кунҷҳои дарунии чилликии дигар ҷуфти кунҷҳо ҳам баробаранд ва ҳосили ҷамъи кунҷҳои дарунии яктарафаи ҳар як ҷуфти кунҷҳо ба 180° баробар аст. Инро исбот кунед.
Ҷавоб. Фарз мекунем, ки AB ва CD ду хати рост мебошанд ва бигзор AC хати рости сеюме бошад, ки хатҳои рости AB ва CD-ро мебурад (расми 71). Хати рости AC нисбат ба хатҳои рости AB ва CD хати буранда номида мешавад.
Бурандаи AC бо хатҳои рости AB ва CD ду ҷуфт кунҷҳои дарунии яктарафа ва ду ҷуфт кунҷҳои дарунии чилликӣ ҳосил менамоянд. Кунҷҳои дарунии чилликии як ҷуфт (масалан, \(\angle\)1 ва \(\angle\)2) ба кунҷҳои дарунии чилликии дигар ҷуфт (масалан, \(\angle\)3 ва \(\angle\)4) ҳамсоя мебошанд (расми 72).
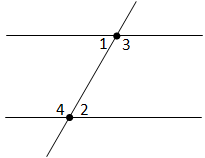
Бигзор \(\angle\)1 = \(\angle\)2 бошад. Азбаски, \(\angle\)1 ва \(\angle\)3 – кунҷҳои ҳамсоя ҳастанд ва \(\angle\)2 ва \(\angle\)4 – ҳам кунҷҳои ҳамсоя ҳастанд, \(\angle\)1 + \(\angle\)3 = 180° ва \(\angle\)2 + \(\angle\)4 = 180° мебошад. Барои он ки, \(\angle\)1 = \(\angle\)2, он гоҳ \(\angle\)1 + \(\angle\)3 = \(\angle\)1 + \(\angle\)4 = 180°. Яъне, \(\angle\)3 ба \(\angle\)4 баробар аст.
Бинобар ин, агар кунҷҳои дарунии чилликии як ҷуфт баробар бошанд, он гоҳ кунҷҳои дарунии чилликии дигар ҷуфт ҳам баробаранд.
Азбаски, \(\angle\)3 = \(\angle\)4 ва \(\angle\)2 + \(\angle\)4 = 180°, он гоҳ \(\angle\)2 + \(\angle\)3 = 180° мебошад. Бинобар ин, агар кунҷҳои дарунии чилликӣ баробар бошанд, он гоҳ ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар аст. Ва баръакс: агар ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар бошад, он гоҳ кунҷҳои дарунии чилликӣ баробаранд.
Саволи 4. Аломати параллели хатҳои ростро исбот кунед.
Ҷавоб. Теоремаи 4.2 (аломати параллели хатҳои рост). Агар кунҷҳои дарунии чилликӣ баробар бошанд ё ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар бошад, он гоҳ хатҳои рост параллеланд.
Исбот. Бигзор хатҳои рости a ва b бо бурандаи AB кунҷҳоидарунии чилликии баробар ташкил диҳанд (расми 73, а). Фарз мекунем, ки хатҳои рости a ва b параллел нестанд, пас, онҳо дар ягон нуқтаи C якдигарро мебуранд (расми 73, б).
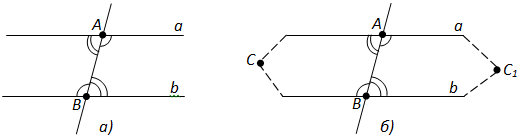
Бурандаи AB ҳамвориро ба ду нимҳамвориҳо тақсим мекунад. Нуқтаи C дар яке аз онҳо воқеъ аст. Дар нимҳамвории дигар секунҷаи BAC1-ро, ки ба секунҷаи ABC баробар аст месозем, C қуллаи он аст. Мувофиқи шарт кунҷҳои дарунии чилликии назди хатҳои рости a, b ва бурандаи AB баробар мебошанд. Азбаски кунҷҳои мувофиқи секунҷаҳои ABC ва BAC1 (қуллаҳояшон A ва B) баробаранд, пас, онҳо бо кунҷҳои дарунии чилликӣ ҳамҷоя мешаванд. Пас, хати рости AC1 бо хати рости a ва хати рости BC1 бо хати рости b ҳамҷоя мешаванд. Аз нуқтаҳои C ва C1 ду хати рост гуногуни a ва b мегузаранд. Ин ғайри имкон аст. Пас, хатҳои рости a ва b параллел мебошанд.
Агар дар хатҳои рости a ва b ва бурандаи AB ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар бошад, он гоҳ, чунон ки медонем, кунҷҳои дарунии чилликӣ баробаранд. Пас, мувофиқи исбот, хатҳои рости a ва b параллел мебошанд. Теорема исбот шуд.
Саволи 5. Чӣ гуна кунҷҳоро кунҷҳои мувофиқ меноманд? Шарҳ диҳед. Агар кунҷҳои чилликӣ баробар бошанд, он гоҳ кунҷҳои мувофиқ ҳам баробаранд, ва баръакс. Инро исбот кунед.
Ҷавоб. 1) Агар дар як ҷуфт кунҷҳои дарунии чилликӣ як кунҷ бо кунҷи ба он амудӣ иваз карда шавад, ҷуфти кунҷҳое ҳосил мешавад, ки онҳоро кунҷҳои мувофиқи хатҳои рости додашудаю буранда меноманд.
2) Бигзор кунҷҳои 1 ва 2 - кунҷҳои дарунии чилликӣ бошанд ва кунҷи 3 ба кунҷи 2 амудӣ бошад (расми 74).
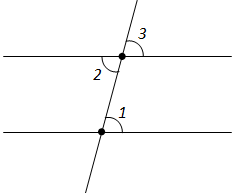
Бинобар теоремаи 2.2 кунҷҳои 2 ва 3 баробар мебошанд. Барои он ки, \(\angle\)1 = \(\angle\)2 ва \(\angle\)2 = \(\angle\)3, \(\angle\)1 = \(\angle\)2 = \(\angle\)3 мешавад. Яъне, \(\angle\)1 = \(\angle\)3 мебошад.
3) Бигзор кунҷҳои 1 ва 3 - кунҷҳои мувофиқ бошанд ва бигзор онҳо баробар бошанд (расми 74). Азбаски кунҷҳои 2 ва 3 - кунҷҳои амудӣ ҳастанд, он гоҳ, бинобар теоремаи 2.2 онҳо баробар ҳастанд. Барои он ки, \(\angle\)1 = \(\angle\)3 ва \(\angle\)2 = \(\angle\)3, \(\angle\)1 = \(\angle\)3 = \(\angle\)2 мешавад. Яъне, \(\angle\)1 = \(\angle\)2 мебошад.
Аз баробарии кунҷҳои дарунии чилликӣ баробарии кунҷҳои мувофиқ натиҷа мешаванд, ва баръакс.
Саволи 6. Аз нуқтае, ки дар хати рости додашуда воқеъ нест, хати рости ба он параллел гузаронидан мумкин аст. Инро исбот кунед. Аз нуқтае, ки дар хати рости додашуда воқеъ нест, чанд хати рости ба он параллел гузаронидан мумкин аст?
Ҷавоб.Фарз мекунем, ки AB – хати рости додашуда ва C – нуқтае, ки дар хати рости AB воқеъ нест. Хати рости AC ҳамвориро ба ду нимҳамворӣ тақсим мекунад (расми 75).
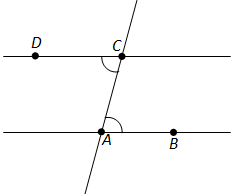
Нуқтаи B дар яке аз онҳо воқеъ аст. Аз нимхати рости CA дар дигар нимҳамворӣ кунҷи ACD-и ба кунҷи CAB баробарро мекашем. Он гоҳ хатҳои рости AB ва CD параллел мешаванд. Ҳақиқатан, барои ин хатҳои рост ва бурандаи AC кунҷҳои BAC ва DCA кунҷҳои дарунии чилликӣ мебошанд. Азбаски ин кунҷҳо баробаранд, пас хатҳои рости AB ва CD параллел мебошанд.
Тасдиқоти фарзамон ва аксиомаи IX (хосияти асосии хатҳои рости параллел)-ро муқоиса карда, ба чунин хулосаи муҳим меоем: аз нуқтае, ки дар хати рост воқеъ нест, хати рости ба хати рости додашуда параллел гузаронидан мумкин аст, ва фақат якто.
Саволи 7. Агар ду хати рости параллел бо хати рости сеюм бурида шаванд, он гоҳ кунҷҳои дарунии чилликӣ баробаранд ва ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар мебошанд. Инро исбот кунед.
Ҷавоб. Теоремаи 4.3 (теоремаи баръакси 4.2). Агар ду хати рости параллел бо хати рости сеюм бурида шаванд, он гоҳ кунҷҳои дарунии чилликӣ баробаранд ва ҳосили ҷамъи кунҳои дарунии яктарафа ба 180° баробар аст.
Исбот.Бигзор a ва b хатҳои рости параллел бошанд ва c хати ростест, ки онҳоро дар нуқтаҳои A ва B мебурад. Аз нуқтаи A хати рости a1-ро чунон мегузаронем, ки кунҷҳои дарунии чилликӣ (бурандаи c ва хатҳои рости a1 ва b ҳосил кардаанд) баробар шаванд (расми 76).
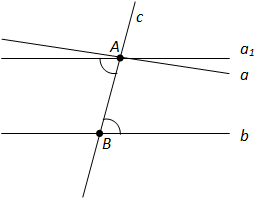
Мувофиқи аломати параллелии хатҳои рост хатҳои рости a1 ва b параллел мебошанд. Азбаски аз нуқтаи A фақат як хати рости ба хати рости b параллел мегузарад, пас хати рости a бо хати рости a1 ҳамҷоя мешавад.
Пас, кунҷҳои дарунии чилликие, ки бурандаю хатҳои ромти параллели a ва b ҳосил кардаанд, баробар мебошанд. Теорема исбот шуд.
Саволи 8. Ду хати росте, ки ба хати рости сеюм перпендикуяр аст, параллел мебошанд. Агар хати рост ба яке аз ду хати рости параллел перпендикуляр бошад, он гоҳ он ба хати рости дигар ҳам перпендикуляр аст. Инро исбот кунед.
Ҷавоб. Бигзор AB ва CD хатҳои росте, ки ба хати рости EF перпендикуляр бошанд. Хати рости EF – буранда аст. Азбаски хатҳои рости перпендикуляр – он хатҳое ҳастанд, ки якдигарро дар таҳти кунҷи рост (90°) мебуранд, кунҷи BEF ба 90° баробар аст ва кунҷи DFE ҳам ба 90° баробар аст. Ҳосили ҷамъи кунҷҳои BEF ва DFE ба 90° + 90°, аниқтар ба 180° баробар аст. Мувофиқи аломати параллелии хатҳои рост, хатҳои рости AB ва CD параллел мебошанд. Яъне, ду хати росте, ки ба хати рости сеюм перпендикуяр аст, параллел мебошанд.
Бигзор AB ва CD хатҳои рости параллел бошанд ва хатҳои рости AB ва EF хатҳои рости перпендикуляр бошанд. Хати рости EF – буранда аст. Азбаски дар хатҳои рости параллеле, ки бо бурандаи EF бурида шудаанд, ҳосили ҷамъи кунҷҳои дарунии яктарафа ба 180° баробар аст ва кунҷи BEF ба 90° баробар аст, кунҷи DFE ба 180° - 90° = 90° баробар аст. Азбаски хатҳои рости перпендикуляр – он хатҳое ҳастанд, ки якдигарро дар таҳти кунҷи рост (90°) мебуранд, хатҳои рости CD ва EF ҳам хатҳои рости перпендикуляр мебошанд. Яъне, агар хати рост ба яке аз ду хати рости параллел перпендикуляр бошад, он гоҳ он ба хати рости дигар ҳам перпендикуляр аст.
Саволи 9. Исбот кунед, ки ҳосили ҷамъи кунҷҳои секунҷа ба 180° баробар аст.
Ҷавоб. Теоремаи 4.4. Ҳосили ҷамъи кунҷҳои секунҷа ба 180° баробар аст.
Исбот.Фарз мекунем, ки ABC секунҷаи додашуда аст. Аз қуллаи B хати рости ба хати рости AC параллелро мегузаронем. Дар он нуқтаи D-ро чунон нишона мекунем, ки нуқтаҳои A ва D аз хати рости BC дар тарафҳои гуногун воқеъ шаванд (расми 78).
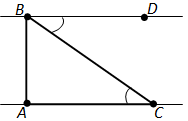
Кунҷҳои DBC ва ACB чун кунҷҳои дарунии чилликӣ (бурандаи BC ва хатҳои рости AC ва BD ҳосил кардаанд) баробаранд. Бинобар ин ҳосили ҷамъи кунҷҳои назди қуллаҳои B ва C-и секунҷа ба кунҷи ABD баробар аст.
Ҳосили ҷамъи кунҷҳои секунҷа ба ҳосили ҷамъи кунҷҳои ABD ва BAC баробар аст. Азбаски ин кунҷҳо барои хатҳои рости параллели AC ва BD ва бурандаи AB кунҷҳои дарунии яктарафа мебошанд, пас ҳосили ҷамъи онҳо ба 180° баробар аст. Теорема исбот шуд.
Саволи 10. Дар секунҷаи дилхоҳ ақаллан ду кунҷи тез ҳаст. Инро исбот кунед.
Ҷавоб. Фарз мекунем, ки секунҷа фақат як кунҷи тез дорад ё, умуман, кунҷҳои тез надорад. Он гоҳ дар ин секунҷа ду кунҷе ҳаст, ки ҳар кадомашон аз 90° хурд нестанд. Ҳосили ҷамъи ин кунҷҳо аз 180° хурд нест. Лекин ин ғайри имкон аст, чунки ҳосили ҷамъи се кунҷи секунҷа ба 180° баробар аст. Яъне, дар секунҷаи дилхоҳ ақаллан ду кунҷи тез ҳаст.
Саволи 11. Кунҷи берунии секунҷа чист?
Ҷавоб. Кунҷе, ки ба кунҷи дар назди қулла воқеъбудаи секунҷа ҳамсоя аст, кунҷи берунии секунҷа (дар назди ҳамон қулла) номида мешавад (расми 79).
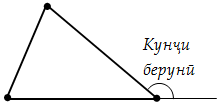
Саволи 12. Кунҷи берунии секунҷа ба ҳосили ҷамъи ду кунҷи дарунии ба он ҳамсоя набудагӣ баробар аст. Инро исбот кунед.
Ҷавоб. Теоремаи 4.5. Кунҷи берунии секунҷа ба ҳосили ҷамъи ду кунҷи дарунии ба он ҳамсоя набудагӣ баробар аст.
Исбот.Фарз мекунем, ки ABC секунҷаи додашуда аст (расми 80).
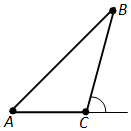
Мувофиқи теоремаи ҳосили ҷамъи кунҷҳои секунҷа \(\angle\)A + \(\angle\)B + \(\angle\)C = 180°.
Аз ин ҷо натиҷа мебарояд, ки \(\angle\)A + \(\angle\)B = 180° - \(\angle\)C.
Дар қисми рости ин баробарӣ ченаки дараҷагии кунҷи берунии секунҷа (назди қуллаи C) ҳаст. Теорема исбот шуд.
Саволи 13. Кунҷи берунии секунҷа аз кунҷи дарунии дилхоҳи ба он ҳамсоя набудагӣ калон аст. Инро исбот кунед.
Ҷавоб. Фарз мекунем, ки ABC секунҷаи додашуда аст. Мувофиқи теоремаи 4.5 кунҷи берунии секунҷа ба \(\angle\)A + \(\angle\)B баробар аст. Азбаски аз рӯи аксиомаи V (хосияти асосии чен кардани кунҷҳо) \(\angle\)A ва \(\angle\)B калон аз 0° буда, аз 180° хурд мебошанд, он гоҳ кунҷҳои A ва B аз кунҷи берунии секунҷа калон буда наметавонанд. Бинобар ин, кунҷҳои ба кунҷи берунии секунҷа ҳамсоя набудагӣ, аз кунҷи берунии секунҷа хурд ҳастанд. Яъне, кунҷи берунии секунҷа аз кунҷи дарунии дилхоҳи ба он ҳамсоя набудагӣ калон аст.
Саволи 14. Чӣ гуна секунҷаро секунҷаи росткунҷа меноманд?
Ҷавоб. Агар секунҷа кунҷи рост дошта бошад, онро секунҷаи росткунҷа меноманд.
Саволи 15. Ҳосили ҷамъи кунҷҳои тези секунҷаи росткунҷа ба чӣ баробар аст?
Ҷавоб. Азбаски ҳосили ҷамъи кунҷҳои секунҷа ба 180° баробар аст, пас дар секунҷаи росткунҷа фақат як кунҷи рост ҳаст. Ду кунҷи дигари секунҷаи росткунҷа кунҷҳои тез мебошанд. Ҳосили ҷамъи кунҳои тези секунҷаи росткунҷа баробари 180° - 90° = 90°.
Саволи 16. Кадом тарафи секунҷаи росткунҷа гипотенуза номида мешавад? Кадом тарафҳо катетҳо номида мешаванд?
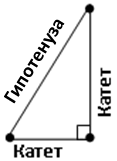
Ҷавоб. Тарафи секунҷаи росткунҷае, ки дар муқобили кунҷи рост ҳаст, гипотенуза номида мешавад; ду тарафи дигар катетҳо номида мешаванд (расми 82).
Саволи 17. Аломати баробарии секунҷаҳои росткунҷаро аз рӯи гипотенуза ва катет баён кунед.
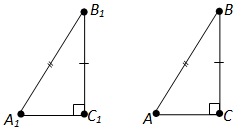
Ҷавоб. Агар гипотенуза ва катети як секунҷаи росткунҷа мувофиқан ба гипотенуза ва катети дигар секунҷаи росткунҷа баробар бошад, он гоҳ ин гуна секунҷаҳо баробаранд (расми 83).
Саволи 18. Аз нуқтаи дилхоҳе, ки дар хати рости додашуда воқеъ нест, ба ин хати рост фақат якто перпендикуляр гузаронидан мумкин аст. Инро исбот кунед.
Ҷавоб. Теоремаи 4.6. Аз нуқтаи дилхоҳе, ки дар хати рости додашуда воқеъ нест, ба ин хати рост перпендикуляр гузаронидан мумкин аст, ва фақат якто.
Исбот.Фарз мекунем, ки a хати рости додашуда ва A нуқтаи дар он воқеъ набудагӣ мебошад (расми 85).
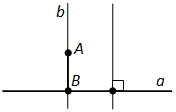
Аз ягон нуқтаи хати рости a хати рости перпендикуляр мегузаронем. Акнун аз нуқтаи A хати рости b-и ба он параллелро мегузаронем. Он ба хати рости a перпендикуляр мешавад, чунки хати рости a, ки ба яке аз хатҳои рости параллел перпендикуляр буд, ба хати рости параллели дигар низ перпендикуляр мебошад. Порчаи AB-и хати рости b перпендикулярест, ки аз нуқтаи A ба хати рости a гузаронида шудааст.
Ягонагии перпендикуляри AB-ро исбот мекунем. Фарз мекунем, ки перпендикуляри дигари AC вуҷуд дорад. Он гоҳ секунҷаи ABC ду кунҷи рости дорад. Лекин ин, чунон ки мо медонем, ғайри имкон аст. Теорема исбот шуд.
Саволи 19. Чиро масофаи байни нуқта ва хати рост меноманд?
Ҷавоб. Дарозии перпендикуляре, ки аз нуқтаи додашуда ба хати рост гузаронида шудааст, масофаи байни нуқта ва хати рост номида мешавад.
Саволи 20. Масофаи байни хатҳои рости параллел чист? Шарҳ диҳед.
Ҷавоб. Масофа аз ягон нуқтаи як хати рост то хати рости дигар масофаи байни хатҳои рости параллел номида мешавад.
