Формулаи биноми Нютон:
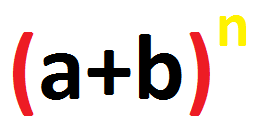
$$(a+b)^n = C_n^0a^n+C_n^1a^{n-1}b+...+C_n^ka^{n-k}b^k+...+C_n^nb^n$$
\((k+1)\) - ум аъзои сумма:
$$T_{k+1}=C_n^ka^{n-k}b^k$$
Суммаи коэффитсиентҳои биномиалӣ ба \(2^n\) баробар аст:
$$C_n^0+C_n^1+...C_n^n=2^n$$
Исботи биноми Нютон:
$$(a+b)^n=(a+b)\cdot(a+b)\cdot...\cdot(a+b)$$
\(a^{n-k}b^k\) - \(C_n^k\) - то
Аз \(n\) қавс \(k\) - то \(b\) интихоб мекунем ва \((n-k)\) - то \(a\) интихоб мекунем. Инро бо \(C_n^k\) роҳ интихоб карда мешавад.
Акнун,
$$C_n^0+C_n^1+...C_n^n=2^n$$-ро исбот мекунем:
$$2^n=(1+1)^n=C_n^01^n+C_n^11^{n-1}1+...+C_n^n1^n=C_n^0+C_n^1+...+C_n^n.$$ Исбот шуд.
