Мавод дар асоси китоби «Геометрия»-и математик А.В. Погорелов тартиб дода шудааст.
Саволи 1. Давра чист? Маркази давра чист? Радиус чист?
Ҷавоб. Шакле, ки аз ҳамаи нуқтаҳои ҳамвории аз нуқтаи додашуда якхел дур буда ташкил шудааст, давра номида мешавад. Ин нуқтаи додашударо маркази давра меноманд. Масофа аз нуқтаҳои давра то маркази онро радиуси давра меноманд. Инчунин порчаи дилхоҳе, ки нуқтаи давраро ба маркази он пайваст мекунад, радиус номида мешавад (расми 90).
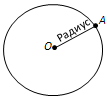
Расми 90
Саволи 2. Хордаи давра чист? Чӣ гуна хордаро диаметр меноманд?
Ҷавоб. Порчае, ки ду нуқтаи давраро пайваст мекунад, хорда номида мешавад. Хордае, ки аз марказ мегузарад, диаметр номида мешавад. Дар расми 91 BC хорда ва AD диаметр мебошад.
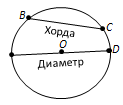
Расми 91
Саволи 3. Чӣ гуна давраро давраи берун кашидашудаи секунҷа меноманд?
Ҷавоб. Агар давра аз ҳамаи қуллаҳои секунҷа гузарад, давраро давраи берун кашидашудаи секунҷа меноманд.
Саволи 4. Маркази даврае, ки дар атрофи секунҷа кашида шудааст, дар буриши перпендикулярҳои миёна ба тарафҳои секунҷа воқеъ аст. Инро исбот кунед.
Ҷавоб. Теоремаи 5.1. Нуқтаи буриши перпендикулярҳо ба тарафҳои секунҷа, ки аз миёнаҷои ин тарафҳо гузаронида шудаанд, маркази давраи берун кашидашудаи секунҷа мебошад.
Исбот. Фарз мекунем, ки ABC секунҷаи додашуда ва O маркази давраи берун кашидашудаи он мебошад (расми 93). Секунҷаи AOC секунҷаи баробарпаҳлӯ аст: тарафҳои он OA ва OC, чун радиусҳо, баробаранд. Медиана OD-и ин секунҷа дар як вақт баландии он мебошад. Бинобар ин маркази давра дар хати росте, ки ба тарафи AC перпендикуляр аст ва аз миёнаҷои он мегузарад, воқеъ аст. Айнан, ҳамин тавр исбот карда мешавад, ки маркази давра дар перпендикулярҳо ба ду тарафи дигари секунҷа воқеъ аст. Теорема исбот шуд. Қайд. Хати ростеро, ки аз миёнаҷои порча ба он перпендикуляр шуда мегузарад, аксар вақт перпендикуляри миёна меноманд. Вобаста ба ин аксар вақт чунин мегӯянд: маркази даврае, ки берун кашидашудаи секунҷа мебошад, дар буриши перпендикулярҳои миёнаи тарафҳои секунҷа воқеъ аст.
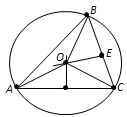
Расми 93
Саволи 5. Чӣ гуна хати ростро расандаи давра меноманд?
Ҷавоб. Хати росте, ки аз нуқтаи давра ба радиус (-и ба ин нуқта гузаронидашуда) перпендикуляр шуда мегузарад, расанда номида мешавад. Дар айни ҳол нуқтаи додашудаи давра нуқтаи расиш номида мешавад. Дар расми 95 хати рости a аз нуқтаи A-и давра ба радиуси OA перпендикуляр карда гузаронида шудааст. Хати рости a расандаи давра мебошад. Нуқтаи A нуқтаи расиш мебошад. Инчунин гуфтан мумкин, ки хати рости a дар нуқтаи A ба давра мерасад.
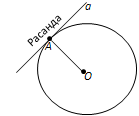
Расми 95
Саволи 6. Давраҳо дар нуқтаи додашуда мерасанд, - чӣ маъно дорад?
Ҷавоб. Ду даврае, ки нуқтаи умумӣ доранд, дар ин нуқта мерасанд, агар онҳо дар ин нуқта расандаи умумӣ дошта бошанд (расми 97).
Саволи 7. Чӣ гуна расиши давра расиши берунӣ номида мешавад? Чӣ гуна расиши давра расиши дарунӣ номида мешавад?
Ҷавоб. Агар маркази давраҳо аз расандаи умумии онҳо дар тарафҳои гуногун воқеъ бошанд, расиши давраҳоро расиши берунӣ меноманд (расми 97, б). Агар маркази давраҳо аз расандаи умумии онҳо дар як тараф воқеъ бошанд, расиши давраҳоро расиши дарунӣ меноманд (расми 97, а).
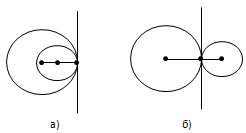
Расми 97
Саволи 8. Чӣ гуна давраро давраи дарун кашидашудаи секунҷа меноманд?
Ҷавоб. Агар давра ба ҳамаи тарафҳои секунҷа расад, давраро давраи дарун кашидашудаи секунҷа меноманд.
Саволи 9. Маркази даврае, ки дарун кашидашудаи секунҷа аст, дар буриши биссектрисаҳои он воқеъ мебошад. Инро исбот кунед.
Ҷавоб. Теоремаи 5.2. Нуқтаи буриши биссектрисаҳои секунҷа маркази давраи дарун кашидашудаи секунҷа мебошад.
Исбот. Фарз мекунем, ки ABC секунҷаи додашуда, O маркази давраи дарун кашидашудаи он, D, E ва F нуқтаҳои расиши давра ба тарафҳо мебошад (расми 98). Секунҷаҳои росткунҷаи AOD ва AOE аз рӯи гипотенуза ва катетҳо баробаранд. Дар ин секунҷаҳо гипотенузаи AO умумӣ буда, катетҳои OD ва OE, чун радиусҳо, баробар мебошанд. Аз баробарии секунҷаҳо натиҷа мебарояд, ки кунҷҳои OAD ва OAE баробаранд. Ин чунин маъно дорад, ки нуқтаи O дар биссектрисаи секунҷа, ки аз қуллаи A гузаронида шудааст, воқеъ мебошад. Айнан ҳамин тавр исбот карда мешавад, ки нуқтаи O дар ду биссектрисаи дигари секунҷа воқеъ мебошад. Теорема исбот шуд.
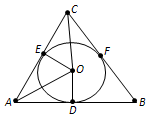
Расми 98
Саволи 10. Секунҷаро аз рӯи се тараф чӣ тавр сохтан мумкин аст? Шарҳ диҳед.
Ҷавоб. Масъалаи 5.1. Секунҷаи тарафҳояш додашудаи a, b, c (расми 99, а) сохта шавад. Ҳал. Бо ёрии хаткашак хати рости дилхоҳ мегузаронем ва дар он нуқтаи B-ро нишона мекунем (расми 99, б). Паргорро ба андозаи баробари a, мекушоем ва давраи марказаш B ва радиусаш a-ро мекашем. Фарз мекунем, ки C нуқтаи буриши давраю хати рост мебошад. Акнун паргорро ба андозаи баробари c кушода, аз маркази B давра мекашем. Паргорро ба андозаи баробари b кушода, аз маркази C давра мекашем. Бигзор A нуқтаи буриши ин давраҳо бошад. Порчаҳои AB ва AC-ро мегузароне. Секунҷаи ABC ҳосил шуд, ки тарафҳояш баробари a, b, c мебошанд.
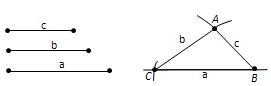
Расми 99
Саволи 11. Аз нимхати рости додашуда (дар нимҳамвории додашуда) кунҷи ба кунҷи маълум баробарро чӣ тавр ҷудо карда кашидан мумкин аст? Шарҳ диҳед.
Ҷавоб. Масъалаи 5.2. Аз нимхати рости додашуда (ба нимҳамвории додашуда) кунҷи ба кунҷи додашуда баробарро ҷудо карда созед. Ҳал. Қуллаи A-и кунҷи додашударо марказ ҳисобида, давраи дилхоҳ мекашем (расми 100, а). Бигзор B ва C нуқтаҳои буриши давраю тарафҳои кунҷ бошанд. Бо радиуси AB давраи марказаш нуқтаи O (нуқтаи ибтидои нимхати рости додашуда)-ро мекашем (расми 100, б). Нуқтаи буриши ин давраю нимхати рости додашударо бо B1 ишорат мекунем. Давраи марказаш B1 ва радиусаш BC-ро мекашем. Нуқтаи буриши давраҳои сохташуда C1 (дар нимҳамвории додашуда) дар тарафи кунҷи матлуб воқеъ аст. Барои исбот қайд кардан кифоя аст, ки секунҷаҳои тарафҳояшон мувофиқан баробар, баробар мебошанд. Кунҷҳои A ва O кунҷҳои мувофиқи ин секунҷаҳо мебошанд.
Саволи 12. Кунҷи додашударо чӣ тавр ба ду қисми баробар тақсим кардан мумкин аст? Шарҳ диҳед.
Ҷавоб. Кунҷро ба ду қисм ҷудо кардан – биссектриса гузаронидан аст. Масъалаи 5.3. Биссектрисаи кунҷи додашуда сохта шавад. Ҳал. Аз қуллаи A-и кунҷи додашуда, чун аз марказ, давраи радиусаш дилхоҳ мекашем (расми 101). Фарз мекунем, ки B ва C нуқтаҳои буриши давраю тарафҳои кунҷ мебошанд. Аз нуқтаҳои B ва C бо ҳамон радиус давраҳо мекашем. D нуқтаи буриши ин ду давра мебошад. Нимхати рости AD-ро мегузаронем. Нури AD биссектриса мебошад, чунки он кунҷи BAC-ро ба ду қисми баробар тақсим мекунад. Ин натиҷаи баробарии секунҷаҳо ABD ва ACD мебошад, ки дар онҳо кунҷҳои DAB ва DAC кунҷҳои мувофиқ мебошанд.
Саволи 13. Порчаро чӣ тавр ба ду қисми баробар тақсим кардан мумкин аст? Шарҳ диҳед.
Ҷавоб. Масъалаи 5.4. Порча ба ду қисми баробар тақсим карда шавад. Ҳал. Фарз мекунем, ки AB порчаи додашуда мебошад (расми 102). Аз нуқтаҳои A ва B бо радиуси AB давра мекашем. C ва C1 нуқтаҳои буриши ин давраҳо мебошанд. Ин нуқтаҳо нисбат ба хати рости AB дар нимҳамвориҳои гуногун воқеъ мебошанд. Порчаи CC1 хати рости AB-ро дар нуқтаи O мебурад. Ин нуқта миёнаҷои порчаи AB мебошад. Ҳақиқатан, мувофиқи аломати сеюми баробарии секунҷаҳо секунҷаҳои CAC1 ва CBC1 баробаранд. Аз ин ҷо натиҷа мебарояд, ки кунҷҳои ACO ва BCO баробаранд. Мувофиқи аломати якуми баробарии секунҷаҳо секунҷаҳои ACO ва BCO баробар мебошанд. Тарафҳои AO ва BO-и ин секунҷаҳо тарафҳои мувофиқ мебошанд, бинобар ин онҳо баробаранд. Ҳамин тариқ, O миёнаҷои порчаи AB мебошад.
Саволи 14. Аз нуқтаи додашуда хати рости ба хати рости додашуда перпендикулярро чӣ тавр гузаронидан мумкин аст? Шарҳ диҳед.
Ҷавоб. Масъалаи 5.5. Аз нуқтаи додашудаи O хати рости ба хати рости додашудаи a перпендикуляр гузаронида шавад.
Ҳал. Ду маврид имкон дорад:
1) нуқтаи O дар хати рости a воқеъ аст;
2) нуқтаи O дар хати рости a воқеъ нест.
Мавриди якумро дида мебароем (расми 103).
Аз нуқтаи O давраи радиусаш дилхоҳ мекашем. Давра хати рости a-ро дар нуқтаҳои A ва B мебурад. Аз нуқтаҳои A ва B давраҳои радиусашон AB-ро мекашем. Нуқтаи C нуқтаи буриши ин давраҳо мебошад. Хати рости матлуб аз нуқтаҳои O ва C мегузарад.
Аз баробарии кунҷҳои назди қуллаи O-и секунҷаҳои ACO ва BCO натиҷа мебарояд, ки хатҳои рости OC ва AB перпендикуляранд. Мувофиқи аломати сеюми баробарии секунҷаҳо секунҷаҳои ACO ва BCO баробар мебошанд.
Мавриди дуюмро дида мебароем (расми 104).
Аз нуқтаи O даврае мекашем, ки он хати рости a-ро мебурад. Бигзор A ва B нуқтаҳои буриши он бо хати рости a бошанд. Аз нуқтаҳои A ва B бо ҳамон радиус давраҳо мекашем. O1 – нуқтаи буриши онҳо, ки назар ба нуқтаи O дар дигар нимҳамворӣ воқеъ аст. Хати рости матлуб аз нуқтаҳои O ва O1 мегузарад. Инро исбот мекунем.
Нуқтаи буриши хатҳои рости AB ва OO1-ро бо C ишорат мекунем. Секунҷаҳои AOB ва AO1B мувофиқи аломати сеюм баробаранд. Бинобар ин кунҷи OAC ва O1AC баробар аст. Онгоҳ секунҷаҳои OAC ва O1AC мувофиқи аломати якум баробар мебошанд. Пас, кунҷҳои онҳо ACO ва ACO1 баробаранд. Азбаски ин кунҷҳо ҳамсоя мебошанд, пас онҳо кунҷҳои ростанд. Ҳамин тариқ , OC перпендикулярест, ки аз нуқтаи O ба хати рости a фуроварда шудааст.
Саволи 15. Ҷои геометрии нуқтаҳое, ки аз ду нуқтаи додашуда як хел дур мебошанд, чиро тасвир мекунанд.
Ҷавоб.Теоремаи 5.3. Ҷои геометрии нуқтаҳое, ки аз ду нуқтаи додашуда якхел дуранд, хати ростест, ки ба порчаи пайвасткунандаи ин нуқтаҳо перпендикуляр буда, аз миёнаҷои он мегузарад.
Исбот. Фарз мекунем, ки A ва B – нуқтаҳои додашуда ва a хати ростест, ки аз миёнаҷой (O)-и порчаи AB мегузараду ба ҳамин порча перпендикуляр аст (расми 105). Мо бояд исбот кунем, ки:
1) ҳар як нуқтаи хати рости a аз нуқтаҳои A ва B якхел дур аст;
2) ҳар як нуқтаи D-и ҳамворӣ, ки аз нуқтаҳои A ва B якхел дурр аст, дар хати рости a воқеъ мебошад.
Аз баробарии секунҷаҳои AOC ва BOC натиҷа мебарояд, ки ҳар як нуқтаи C-и хати рости a аз нуқтаҳои A ва B дар якхел масофа воқеъ мебошанд. Дар секунҷаҳои AOC ва BOC кунҷҳои назди қуллаи O кунҷҳои рост мебошанд, тарафи OC – тарафи умумӣ ва AO = OB, чунки O миёнаҷои порчаи AB аст.
Акнун нишон медиҳем, ки ҳар як нуқтаи D-и ҳамворӣ, ки аз нуқтаҳои A ва B якхел дуранд, дар хати рости a воқеъ мебошанд. Секунҷаи ADB-ро дида мебароем. ADB секунҷаи баробарпаҳлӯ аст, чунки AD = BD. Дар он DO – медиана. Мувофиқи хосияти секунҷаи баробарпаҳлӯ медианае, ки ба асос гузаронида шудааст, баландӣ мебошад. Пас, нуқтаи D дар хати рости a воқеъ аст. Теорема исбот шуд.
