Барои дар маҳал чен кардани масофаи байни ду нуқтаи \(A\) ва \(B\), ки аз байнашон (аз рӯи хати рост) гузаштан мумкин нест, чунин нуқтаи \(C\)-ро интихоб мекунанд, ки аз он ҳам ба нуқтаи \(A\) ва ҳам ба нуқтаи \(B\) рафтан мумкин аст ва аз \(C\) ҳардуи ин нуқтаҳо намоён аст. Самти масофаҳои \(AC\) ва \(BC\)-ро бо ходаҳо нишона мекунанд. \(AC\) ва \(BC\)-ро ба паси нуқтаи \(C\) давом медиҳанд ва \(CD = AC\) ва \(EC = CB\)-ро чен мекунанд. Он гоҳ порчаи \(ED\) ба масофаи матлуб баробар мешавад. Чаро ин давр шуд? Фаҳмонед.
Ҳал.
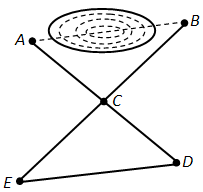
Ду секунҷа ҳосил мешавад: \(\triangle ABC = \triangle DEC\). Мувофиқи шарти масъала дар ин секунҷаҳо \(AC = CD, BC = CE\) мебошанд. Азбаски кунҷҳои \(ACB\) ва \(DCE\) вертикалӣ ҳастанд, пас \(\angle ACB = \angle DCE\). Яъне, бо назардошти аломати якуми баробарии секунҷаҳо, секунҷаҳои ABC ва DEC баробар мебошанд. Аз баробарии секунҷаҳои \(ABC\) ва \(DEC\) мебарояд, ки \(DE = AB\). Яъне, дарозии порчаи \(DE\) ба масофаи матлуб баробар мешавад.
