Дар тарафи \(AB\)-и секунҷаи \(ABC\) нуқтаи \(D\) ва дар тарафи \(A_1B_1\)-и секунҷаи \(A_1B_1C_1\) нуқтаи \(D_1\) нишона карда шудааст. Маълум, ки секунҷаҳои \(ADC\) ва \(A_1D_1C_1\) баробаранд. Порчаҳои \(DB\) ва \(D_1B_1\) ҳам баробаранд. Баробарии секунҷаҳои \(ABC\) ва \(A_1B_1C_1\)-ро исбот кунед.
Ҳал.
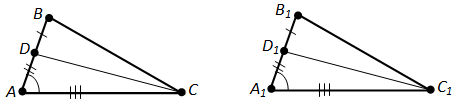
Аз \(\triangle ADC = \triangle A_1D_1C_1\) мебарояд, ки \(AD = A_1D_1\).
Мувофиқи шарти масъала \(DB = D_1B_1\) аст.
Азбаски нуқтаи \(D\) дар порчаи \(AB\) воқеъ аст, пас \(AB = AD + DB\).
Азбаски нуқтаи \(D_1\) дар порчаи \(A_1B_1\) воқеъ аст, пас \(A_1B_1 = A_1D_1 + D_1B_1\).
\(AB = AD + DB = A_1D_1 + D_1B_1 = A_1B_1\)
Пас, \(AB = A_1B_1\) аст.
Аз \(\triangle ADC = \triangle A_1D_1C_1\) мебарояд, ки \(AC = A_1C_1\).
Аз \(\triangle ADC = \triangle A_1D_1C_1\) мебарояд, ки \(\angle A = \angle A_1\).
Мувофиқи аломати якуми баробарии секунҷаҳо \(\triangle ABC = \triangle A_1B_1C_1\).
