Порчаҳои \(AC\) ва \(BD\) дар нуқтаи \(O\) якдигарро мебуранд. Маълум, ки кунҷи \(BAO\) ба кунҷи \(DCO\) баробар аст ва \(AO = CO\). Баробарии секунҷаҳои \(BAO\) ва \(DCO\)-ро исбот кунед.

Ҳал.

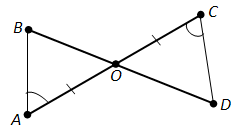
Секунҷаҳои \(BAO\) ва \(DCO\) аз рӯи аломати дуюми баробарии секунҷаҳо баробар мебошанд. Дар ҳақиқат, дар онҳо мувофиқи шарти масъала \(AO = CO\), \(\angle BAO = \angle DCO\) ва кунҷҳои \(\angle AOB\) ва \(\angle DOC\) ҳамчун кунҷҳои вертикалӣ баробаранд.