Периметр равнобедренного треугольника равен 7,5 м, а боковая сторона равна 2 м. Найдите основание.
Решение:
Пусть ABC - данный равнобедренный треугольник с боковыми сторонами AC и BC и основанием AB. Периметр треугольника равен сумме длин его сторон: P = a + b + c, то есть P\(\triangle\)ABC = AC + BC + AB. Так как в равнобедренном треугольнике боковые стороны равны, то P\(\triangle\)ABC = 2AC + AB и P\(\triangle\)ABC = 2 \(\cdot\) 2 + AB.

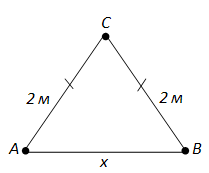
Пусть x - длина основания, тогда:
2 \(\cdot\) 2 + x = 7,5
4 + x = 7,5
x = 7,5 - 4
x = 3,5 - длина основания.
Ответ: длина основания треугольника ABC равна 3,5 м.