Чтобы измерить на местности расстояние между двумя точками A и B, между которыми нельзя пройти по прямой (рис. 58), выбирают такую точку C, из которой можно пройти и к точке A, и к точке B и из которой видны обе эти точки. Провешивают расстояния AC и BC, продолжают их за точку C и отмеряют CD = AC и EC = CB. Тогда отрезок ED равен искомому расстоянию. Объясните почему.
Решение:

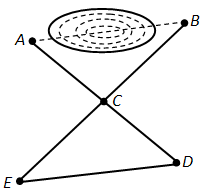
Получаем 2 треугольника: \(\triangle\)ABC и \(\triangle\)DEC. У них AC = CD, BC = CE по условию, а углы ACB и DCE равны как вертикальные. Значит, треугольники ABC и DEC равны по первому признаку равенства треугольников. Из равенства треугольников ABC и DEC следует, что DE = AB. То есть DE равен искомому расстоянию.