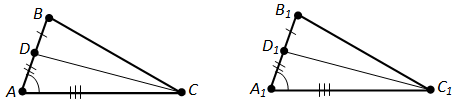
На стороне AB треугольника ABC взята точка D, а на стороне A1B1 треугольника A1B1C1 взята точка D1. Известно, что треугольники ADC и A1D1C1 равны и отрезки DB и D1B1 равны. Докажите равенство треугольников ABC и A1B1C1.
Решение:
Из равенства треугольников ADC и A1D1C1 следует, что \(\angle\)A = \(\angle\)A1, AC = A1C1, AD = A1D1. Так как AD = A1D1 и DB = D1B1 по условию, то AB = AD + DB = A1D1 + D1B1 = A1B1. Треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников. У них \(\angle\)A = \(\angle\)A1, AC = A1C1 и AB = A1B1.