Вопрос 11. Какое преобразование называется симметрией относительно данной прямой?
Ответ. Преобразование фигуры F в фигуру F', при котором каждая еë точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g (рис. 192).

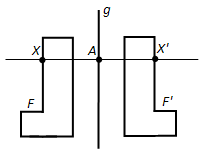
Вопрос 12. Какая фигура называется симметричной относительно данной прямой?
Ответ. Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

Вопрос 13. Что такое ось симметрии фигуры? Приведите пример.
Ответ.Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

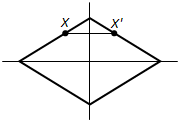
Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, являются осями симметрии прямоугольника (рис.193). Прямые, на которых лежат диагонали ромба, являются его осями симметрии (рис. 194).

Вопрос 14. Докажите, что симметрия относительно прямой есть движение.
Ответ. Теорема 9.3. Преобразование симметрии относительно прямой является движением.
Доказательство.Примем данную прямую за ось y декартовой системы координат (рис. 195). Пусть произвольная точка A (x; y) фигуры F переходит в точку A' (x'; y') фигуры F'. Из определения симметрии относительно прямой следует, что у точек A и A' равные ординаты, а абсцисы отличаются знаком: x' = —x.

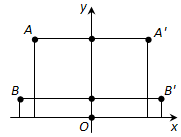
Возьмëм две произвольные точки A' (x₁; y₁) и B (x₂; y₂). Они перейдут в точки A' (—x₁; y₁) и B' (—x₂; y₂).
Имеем: AB2 = (x₂ - x₁)2 + (y₂ - y₁)2,
A'B'2 = (—x₂ + x₁)2 + (y₂ - y₁)2.
Отсюда видно, что AB = A'B'. А это значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.

Вопрос 15. Какое движение называется поворотом?
Ответ. Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении (рис. 196).

Вопрос 16. Что такое параллельный перенос?
Ответ. Параллельный перенос есть движение.

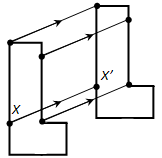
Вопрос 17. Какие вы знаете свойства параллельного переноса?
Ответ. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. При параллельном переносе прямая переходит в параллельную прямую (или в себя).

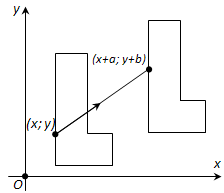
Вопрос 18. Докажите существование и единственность параллельного переноса, переводящего данную точку в другую данную точку.
Ответ. Теорема 9.4. Каковы бы ни были две точки A и A', существует один и только один параллельный перенос, при котором точка A переходит в точку A'.
Доказательство. Начнëм с доказательства существования параллельного переноса, переводящего точку A в A'. Введëм декартовы координаты на плоскости. Пусть a₁,a₂ - координаты точки A и a'₁,a'₂ - координаты точки A'. Параллельный перенос, заданный формулами
x' = x + a'₁ - a₁, y' = y + a'₂ - a₂,
переводит точку A в точку A'. Действительно, при x = a₁ и y = a₂ получаем x' = a'₁, y' = a'₂.

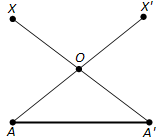
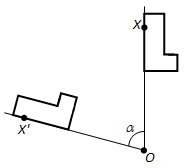
Докажем единственность параллельного переноса, переводящего точку A в точку A'. Пусть X — произвольная точка фигуры и X' — точка,в которую она переходит при параллельном переносе (рис. 202). Как мы знаем, отрезки XA' и AX' имеют общую середину O. Задание точки X однозначно определяет точку O — середину отрезка A'X. А точки A и O однозначно определяют точку X', так как точка O является серединой отрезка AX'. Однозначность в определении точки X' и означает единственность параллельного переноса.
Теорема доказана.

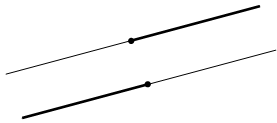
Вопрос 19. Какие полупрямые называются одинаково направленными?
Ответ. Две полупрямые называются одинаково направленными, или сонаправленными, если они совмещаются параллельным переносом. То есть существует параллельный перенос, который переводит одну полупрямую в другую.

Вопрос 20. Докажите, что если полупрямые a и b одинаково направлены и полупрямые b и c одинаково направлены, то полупрямые a и c тоже одинаково направлены.
Ответ. Если полупрямые a и b одинаково направлены и полупрямые b и c одинаково направлены, то полупрямые a и c тоже одинаково направлены (рис. 203).

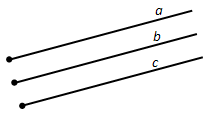
Действительно, пусть параллельный перенос, задаваемый формулами
x' = x + m, y' = y + n, (*)
переводит полупрямую a в полупрямую b, а параллельный перенос, задаваемый формулами
x'' = x' + m₁, y'' = y' + n₁, (**)
переводит полупрямую b в полупрямую c.
Рассмотрим параллельный перенос, задаваемый формулами
x'' = x + m + m₁, y'' = y + n + n₁. (***)
Утверждаем, что этот параллельный перенос переводит полупрямую a в полупрямую c. Докажем это.
Пусть (x; y) — произвольная точка полупрямой a. Согласно формулам (*) точка (x + m; y + n) принадлежит полупрямой b. Так как точка (x + m; y + n) принадлежит полупрямой b, то согласно формулам (***) точка (x + m + m₁; y + n + n₁) принадлежит полупрямой c. Таким образом, параллельный перенос, задаваемый формулами (***), переводит полупрямую a в полупрямую c. А это значит, что полупрямые a и c одинаково направлены, что и требовалось доказать.

Вопрос 21. Какие полупрямые называются противоположно направленными?

Ответ. Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой (рис. 204).

Вопрос 22. Какие фигуры называются равными?
Ответ. Две фигуры называются равными, если они движением переводятся одна в другую.