Глава 10. Задача 3. Дискретная случайная величина $X$ задана законом распределения

Построить график функции распределения этой величины.

Решение.

Если $x \leq 2$, то $F(x) = 0$ (третье свойство).

Если $2 < x \leq 6$, то $F(x) = 0,5$. Действительно, $X$ может принять значение 2 с вероятностью 0,5.

Если $6 < x \leq 10$, то $F(x) = 0,9$. Действительно, если $x_1$ удовлетворяет неравенству $6 < x \leq 10$, то $F(x_1)$ равно вероятности события $X < x_1$, которое может быть осуществлено, когда $X$ примет значение 2 (вероятность этого события равна 0,5) или значение 6 (вероятность этого события равна 0,4). Поскольку эти два события несовместны, то по теореме сложения вероятность события $X < x_1$ равна сумме вероятностей 0,5 + 0,4 = 0,9.

Если $x > 10$, то $F(x) = 1$. Действительно, событие $X \leq 10$ достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

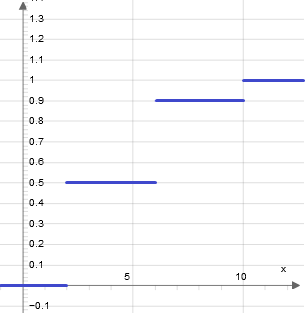
$F(x) = \left\{ \begin{array}{llll}  0\quad при\quad x\leq 2, \\ 0,5\quad при\quad 2 < x \leq 6, \\ 0,9\quad при\quad 6 < x \leq 10, \\ 1\quad при\quad x > 10. \end{array} \right.$

График этой функции: