От вершины C равнобедренного треугольника ABC с основанием AB отложены равные отрезки: CA₁ на стороне CA и CB₁ на стороне CB. Докажите равенство треугольников: 1) CAB₁ и CBA₁; 2) ABB₁ и BAA₁.
Решение:

1) Треугольники CAB₁ и CBA₁ по первому признаку равенства треугольников. У них \(\angle\)C - общий, AC и BC равны как боковые, а CA₁ и CB₁равны по условию.

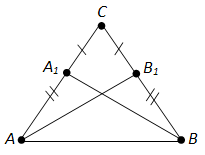
2) Треугольники ABB₁ и BAA₁ по первому признаку равенства треугольников. У них AB - общая сторона, углы CAB и CBA равны как углы при основании. Так как AC = BC и A₁C = B₁C, то из аксиомы III следует, что AC = A₁C + AA₁ и BC = B₁C + BB₁, т. е. AC = A₁C + AA₁ = A₁C + BB₁. Поэтому, AA₁ равен BB₁.