Докажите, что у равностороннего треугольника все углы равны.
Решение:

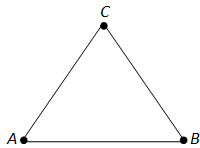
Пусть ABC - данный треугольник с равными сторонами: AB = BC = CA (рис. 49). Так как AB = BC, то этот треугольник равнобедренный с основанием AC. По теореме 3.3 \(\angle\)C = \(\angle\)A. Так как BC = CA, то треугольник ABC равнобедренный с основанием AB. По теореме 3.3 \(\angle\)A = \(\angle\)B. Таким образом, \(\angle\)C = \(\angle\)A = \(\angle\)B, т. е. все углы треугольника равны. Всё что требовалось доказать.