Вопрос 1. Что такое окружность, центр окружности, радиус?
Ответ. Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка называется центром окружности.
Расстояние от точек окружности до её центра называется радиусом. Радиусом называется также любой отрезок, соединяющий точку окружности с её центром.
Вопрос 2. Что такое хорда окружности? Какая хорда называется диаметром?
Ответ. Отрезок, соединяющий две точки окружности, называется хордой. Хорда проходящая через центр, называется диаметром.
Вопрос 3. Какая окружность называется описанной около треугольника?
Ответ. Окружность называется описанной около треугольника, если она проходит через все его вершины.
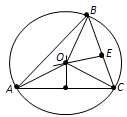
Вопрос 4. Докажите, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Ответ. Теорема 5.1. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон.
Доказательство. Пусть ABC – данный треугольник и O – центр описанной около него окружности (рис. 93). Треугольник AOC равнобедренный: у него стороны OA и OC равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через её середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника. Теорема доказана.

Вопрос 5. Какая прямая называется касательной к окружности?
Ответ. Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведённому в эту точку, называется касательной. При этом данная точка окружности называется точкой касания.
Вопрос 6. Что значит: окружности касаются в данной точке?
Ответ. Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 97).
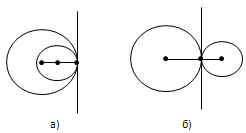
Вопрос 7. Какое касание окружностей называется внешним, какое – внутренним?
Ответ. Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 97, а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 97, б).

Вопрос 8. Какая окружность называется вписанной в треугольник?
Ответ. Окружность называется вписанной в треугольник, если она касается всех его сторон.
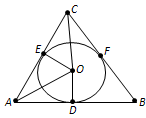
Вопрос 9. Докажите, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Ответ. Теорема 5.2. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Доказательство. Пусть ABC – данный треугольник, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами (рис. 98). Прямоугольные треугольники AOD и AOE равны по гипотенузе и катету. У них гипотенуза AO общая, а катеты OD и OE равны как радиусы. Из равенства треугольников следует равенство углов OAD и OAE. А это значит, что точка O лежит на биссектрисе треугольника, проведённой из вершины A. Точно так же доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.

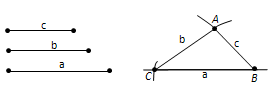
Вопрос 10. Объясните, как построить треугольник по трём сторонам.
Ответ. Задача 5.1. Построить треугольник с данными сторонами a, b, c (рис. 99, а).
Решение. С помощью линейки проводим произвольную прямую и отмечаем на ней произвольную точку B (рис. 99, б). Раствором циркуля, равным a, описываем окружность с центром B и радиусом a. Пусть C – точка её пересечения с прямой. Теперь раствором циркуля, равным c, описываем окружность из центра B, а раствором циркуля, равным b, описываем окружность из центра C. Пусть A – точка пересечения этих окружностей. Проведём отрезки AB и AC. Треугольник ABC имеет стороны, равные a, b, c. Что и требовалось оъяснить.
Вопрос 11. Объясните, как отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.
Ответ. Задача 5.2. Отложить от данной полупрямой в данную полуплоскость угол, равный данному углу.
Решение. Проведём произвольную окружность с центром в вершине A данного угла (рис.100,а). Пусть B и C – точки пересечения окружности со сторонами угла. Радиусом AB проведём окружность с центром в точке O – начальной точке данной полупрямой (рис.100,б). Точку пересечения этой окружности с данной полупрямой обозначим B1. Опишем окружность с центром B1 и радиусом BC. Точка C1 пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.
Для доказательства достаточно заметить, что треугольники ABC и OB1C1 равны как треугольники с соответственно равными сторонами. Углы A и O являются соответствующими углами этих треугольников. Что и требовалось объяснить.
Вопрос 12. Объясните, как разделить данный угол пополам.
Ответ. Задача 5.3. Построить биссектрису данного угла.
Решение. Из вершины A данного угла как из центра описываем окружность произвольного радиуса (рис. 101). Пусть B и C – точки её пересечения со сторонами угла. Из точек B и C тем же радиусом описываем окружности. Пусть D – точка их пересечения, отличная от A. Проводим полупрямую AD.
Луч AD является биссектрисой, так как делит угол BAC пополам. Это следует из равенства треугольников ABD и ACD, у которых углы DAB и DAC являются соответствующими. Что и требовалось объяснить.
Вопрос 13. Объясните, как разделить отрезок пополам.
Ответ. Задача 5.4. Разделить отрезок пополам.
Решение. Пусть AB – данный отрезок (рис. 102). Из точек A и B радиусом AB описываем окружности. Пусть C и C1 – точки пересечения этих окружностей. Они лежат в разных полуплоскостях относительно прямой AB. Отрезок CC1 пересекает прямую AB в некоторой точке O. Эта точка есть середина отрезка AB.
Действительно, треугольники CAC1 и CBC1 равны по третьему признаку равенства треугольников. Отсюда следует равенство углов ACO и BCO. Треугольники ACO и BCO равны по первому признаку равенства треугольников. Стороны AO и BO этих треугольников являются соответствующими, а поэтому они равны. Таким образом, O – середина отрезка AB. Что и требовалось объяснить.
Вопрос 14. Объясните, как через данную точку провести прямую, перпендикулярную данной прямой.
Ответ. Задача 5.5. Через данную точку O провести прямую, перпендикулярную данной прямой a.
Решение. Возможны два случая:
1) точка O лежит на прямой a;
2) точка O не лежит на прямой a.
Рассмотрим первый случай (рис. 103).
Из точки O проводим произвольным радиусом окружность. Она пересекает прямую a в двух точках: A и B. Из точек A и B проводим окружности радиусом AB. Пусть C – точка их пересечения. Искомая прямая проходит через точки O и C.
Перпендикулярность прямых OC и AB следует из равенства углов при вершине O треугольников ACO и BCO. Эти треугольники раны по третьему признаку равенства треугольников.
Рассмотрим второй случай (рис. 104).
Из точки O проводим окружность, пересекающую прямую a. Из точек A и B тем же радиусом проводим окружности. Пусть O1 – точка их пересечения, лежащая в полуплоскости, отличной от той, в которой лежит точка O. Искомая прямая проходит через точки O и O1. Докажем это.
Обозначим через C точку пересечения прямых AB и OO1. Треугольники AOB и AO1B равны по третьему признаку. Поэтому угол OAC равен углу O1AC. А тогда треугольники OAC и O1AC равны по первому признаку. Значит, их углы ACO и ACO1 равны. А так как они смежные, то они прямые. Таким образом, OC – перпендикуляр, опущенный из точки O на прямую a. Что и требовалось объяснить.
Вопрос 15. Что представляет собой геометрическое место точек, равноудалённых от двух данных точек?
Ответ. Теорема 5.3. Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.
Доказательство. Пусть A и B – данные точки, a – прямая, проходящая через середину O отрезка AB перпендикулярно к нему (рис. 105). Мы должны доказать, что:
1) Каждая точка прямой a равноудалена от точек A и B;
2) Каждая точка D плоскости, равноудаленная от точек A и B, лежит на прямой a.
То, что каждая точка C прямой a находится на одинаковом расстоянии от точек A и B, следует из равенства треугольников AOC и BOC. У этих треугольников углы при вершине O прямые, сторона OC общая, а AO=OB, так как O – середина отрезка AB.
Покажем теперь, что каждая точка D плоскости, равноудаленная от точек A и B, лежит на прямой a. Рассмотрим треугольник ADB. Он равнобедренный, так как AD=BD. В нем DO – медиана. По свойству равнобедренного треугольника медиана, проведенная к основанию, является высотой. Значит, точка D лежит на прямой a. Теорема доказана.
