Вопрос 11. Докажите, что для любых векторов \(\overline{a}\) и \(\overline{b}\)
\(\overline{a} + \overline{b} = \overline{b} + \overline{a}\).
Ответ. Для любых векторов \(\overline{a}(a₁; a₂)\), \(\overline{b} (b₁; b₂)\)

\(\overline{a} + \overline{b} = \overline{b} + \overline{a}\).

Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.

Вопрос 12. Докажите, что для любых трёх векторов \(\overline{a}\), \(\overline{b}\), \(\overline{c}\)
\(\overline{a} + (\overline{b} + \overline{c}) = (\overline{a} + \overline{b}) + \overline{c}\).
Ответ. Для любых векторов \(\overline{a}(a₁; a₂)\), \(\overline{b} (b₁; b₂)\), \(\overline{c} (c₁; c₂)\)

\(\overline{a} + (\overline{b} + \overline{c}) = (\overline{a} + \overline{b}) + \overline{c}\).

Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.

Вопрос 13. Докажите векторное равенство \(\overline{AB} + \overline{BC} = \overline{AC}\).
Ответ. Теорема 10.1. Каковы бы ни были точки A, B, C, имеет место векторное равенство

\(\overline{AB} + \overline{BC} = \overline{AC}\).

Доказательство. Пусть A (x₁; y₁), B (x₂; y₂), C (x₃; y₃) – данные точки (рис. 215). Вектор \(\overline{AB}\) имеет координаты x₃ - x₂, y₃ - y₂. Следовательно, вектор \(\overline{AB} + \overline{BC}\) имеет координаты x₃ - x₁, y₃ - y₁. А это есть координаты вектора \(\overline{AC}\). Значит, векторы \(\overline{AB} + \overline{BC}\) и \(\overline{AC}\) равны. Теорема доказана.

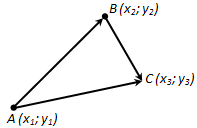
Вопрос 14. Докажите, что для получения суммы векторов \(\overline{a}\) и \(\overline{b}\) надо от конца вектора \(\overline{a}\) отложить вектор \(\overline{b'}\), равный \(\overline{b}\). Тогда вектор, начало которого совпадает с началом вектора \(\overline{a}\), а конец – с концом вектора \(\overline{b'}\), равен \(\overline{a} + \overline{b}\).
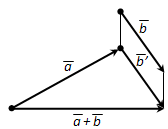
Ответ. Для доказательства достаточно изучить теорему 10.1, которая даёт следующий способ построения суммы произвольных векторов \(\overline{a}\) и \(\overline{b}\). Надо от конца вектора \(\overline{a}\) отложить вектор \(\overline{b'}\), равный вектору \(\overline{b}\). Тогда вектор, начало которого совпадает с началом вектора \(\overline{a}\), а конец – с концом вектора \(\overline{b'}\), будет суммой векторов \(\overline{a}\) и \(\overline{b}\) (рис. 216). Такой способ получения суммы двух векторов называется «правилом треугольника» сложения векторов.

Вопрос 15. Сформулируйте «правило параллелограмма» сложения векторов.
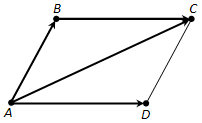
Ответ. Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах ("правило параллелограмма", рис. 217). Действительно, \(\overline{AB} + \overline{BC} = \overline{AC}\), а \(\overline{BC} = \overline{AD}\). Значит, \(\overline{AB} + \overline{AD} = \overline{AC}\).

Вопрос 16. Дайте определение разности векторов.
Ответ. Разностью векторов \(\overline{a}\) (a₁; a₂) и \(\overline{b}\) (b₁; b₂) называется такой вектор \(\overline{c}\) (c₁; c₂), который в сумме с вектором \(\overline{b}\) даëт вектор \(\overline{a}\): \(\overline{b} + \overline{c} = \overline{a}\). Отсюда находим координаты вектора \(\overline{c} = \overline{a} – \overline{b}\):

c₁ = a₁ - b₁; c₂ = a₂ - b₂.

Вопрос 17. Дайте определение умножения вектора на число.
Ответ. Произведением вектора (a₁; a₂) на число \(\lambda\) называется вектор \(\overline{\lambda\)a₁; \(\lambda\)a₂}), т.е. \((\overline{a₁; a₂}) \lambda = (\overline{\lambda a₁; \lambda a₂})\).
По определению \((\overline{a₁; a₂}) \lambda = \lambda (a₁; a₂)\).
Из определения операции умножения вектора на число следует, что для любого вектора \(\overline{a}\) и чисел \(\lambda\), \(\mu\)

\((\lambda + \mu) \overline{a} = \lambda \overline{a} + \mu \overline{a}\).

Для любых двух векторов \(\overline{a}\) и \(\overline{b}\) и числа \(\lambda\)

\(\lambda (\overline{a} + \overline{b}) = \lambda \overline{a} + \lambda \overline{b}\).

Вопрос 18. Докажите, что абсолютная величина вектора \(\lambda \overline{a}\) равна |\(\lambda\)| |\(\overline{a}\)|, направление вектора \(\lambda \overline{a}\) при \(\overline{a} \neq \overline{0}\) совпадает с направлением вектора \(\overline{a}\), если \(\lambda > 0\), и противоположно направлению вектора \(\overline{a}\), если \(\lambda < 0\).
Ответ. Теорема 10.2 Абсолютная величина вектора \(\lambda \overline{a}\) равна |\(\lambda\)| |\(\overline{a}\)|, направление вектора \(\lambda \overline{a}\) при \(\overline{a} \neq \overline{0}\) совпадает с направлением вектора \(\overline{a}\), если \(\lambda > 0\), и противоположно направлению вектора \(\overline{a}\), если \(\lambda < 0\).
Доказательство. Построим векторы \(\overline{OA}\) и \(\overline{OB}\), равные \(\overline{a}\) и \(\lambda \overline{a}\) соответственно (O – начало координат). Пусть a₁ и a₂ - координаты вектора \(\overline{a}\). Тогда координатами точки A будут числа a₁ и a₂, а координатами точки B будут \(\lambda a₁\), \(\lambda a₂) (рис. 222). Уравнение прямой OA имеет вид:

\(\alpha x + \beta y = 0\).

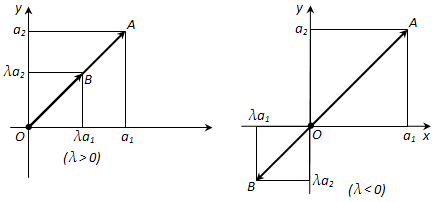
Так как уравнению удовлетворяют координаты точки A (a₁; a₂), то ему удовлетворяют и координаты точки B (\(\lambda a₁; \lambda a₂\)). Отсюда следует, что точка B лежит на прямой OA. Координаты c₁ и c₂ любой точки C, лежащей на полупрямой OA, имеют те же знаки, что и координаты a₁ и a₂ точки A, а координаты любой точки, которая лежит на полупрямой, дополнительной к OA, имеют противоположные знаки.
Поэтому если \(\lambda > 0\), то точка B лежит на полупрямой OA, а следовательно, векторы \(\overline{a}\) и \(\lambda \overline{a}\) одинаково направлены. Если \(\lambda < 0\), то точка B лежит на дополнительной полупрямой, векторы \(\overline{a}\) и \(\lambda \overline{a}\) противоположно направлены. Абсолютная величина вектора \(\lambda \overline{a}\) равна:

\(|\lambda \overline{a}| = \sqrt{(\lambda a₁)^2 + (\lambda a₂)^2} = |\lambda| \sqrt{a^2₁ + a^2₂} = |\lambda| |\overline{a}|\).

Теорема доказана.

Вопрос 19. Какие векторы называются коллинеарными?
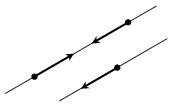
Ответ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (рис. 223). Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.

Вопрос 20. Докажите, что если векторы \(\overline{a}\) и \(\overline{b}\) отличны от нулевого вектора и не коллинеарны, то любой вектор \(\overline{c}\) можно представить в виде \(\overline{c} = \lambda \overline{a} + \mu \overline{b}\).
Ответ. Пусть \(\overline{a}\) и \(\overline{b}\) – отличные от нуля неколлинеарные векторы. Докажем, что любой вектор \(\overline{c}\) можно представить в виде

\(\overline{c} = \lambda \overline{a} + \mu \overline{b}\).

Пусть A и B – начало и конец вектора \(\overline{c}\) (рис. 224). Проведём через точки A и B прямые, параллельные векторам \(\overline{a}\) и \(\overline{b}\). Они пересекутся в некоторой точке C. Имеем:

\(\overline{AB} = \overline{AC} + \overline{CB}\).

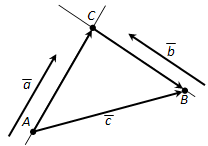
Так как векторы \(\overline{a}\) и \(\overline{AC}\) коллинеарны, то \(\overline{AC} = \lambda \overline{a}\). Так как векторы \(\overline{CB}\) и \(\overline{b}\) коллинеарны, то \(\overline{CB} = \mu \overline{b}\). Таким образом,

\(\overline{c} = \lambda \overline{a} + \mu \overline{b}\),

что и требовалось доказать.

Вопрос 21. Дайте определение скалярного произведения векторов.
Ответ. Скалярным произведением векторов a (a₁; a₂) и b (b₁; b₂) называется число a₁b₁ + a₂b₂.
Для скалярного произведения векторов используется такая же запись как и для произведения чисел. Скалярное произведение \(\overline{a} \cdot \overline{a}\) обозначается a₂и называется скалярным квадратом. Очевидно, \(\overline{a^2} = |\overline{a^2}|\).

Вопрос 22. Докажите, что для любых трёх векторов \(\overline{a}\), \(\overline{b}\), \(\overline{c}\)
\((\overline{a} + \overline{b}) \overline{c} = \overline{a} \overline{c} + \overline{b} \overline{c}\).
Ответ. Из определения скалярного произведения векторов следует, что для любых векторов \(\overline{a}\) (a₁; a₂), \(\overline{b}\) (b₁; b₂), \(\overline{c}\) (c₁; c₂)

\((\overline{a} + \overline{b}) \overline{c} = \overline{a} \overline{c} + \overline{b} \overline{c}\).

Действительно, левая часть равенства есть (a₁ + b₁) c₁ + (a₂ + b₂) c₂, а правая a₁c₁ + a₂c₂ + b₁c₁ + b₂c₂. Очевидно, они равны.

Вопрос 23. Как определяется угол между векторами?
Ответ. Углом между ненулевыми векторами \(\overline{AB}\) и \(\overline{AC}\) называется угол BAC. Углом между любыми двумя ненулевыми векторами \(\overline{a}\) и \(\overline{b}\) называется угол между равными им векторами с общим началом.

Вопрос 24. Чему равен угол между одинаково направленными векторами?
Ответ. Угол между одинаково направленными векторами считается равным нулю.

Вопрос 25. Докажите, что скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Ответ. Теорема 10.3 Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство. Пусть \(\overline{a}\) и \(\overline{b}\) — данные векторы и \(\phi\) — угол между ними. Имеем:

\((\overline{a} + \overline{b})^2 = (\overline{a} + \overline{b}) (\overline{a} + \overline{b}) = (\overline{a} + \overline{b})\overline{a} + (\overline{a} + \overline{b})\overline{b} = \overline{a}\overline{a} + \overline{b}\overline{a} + \overline{a}\overline{b} + \overline{b}\overline{b} = \overline{a^2} + 2\overline{a}\overline{b} + \overline{b^2}\),

или

\(|\overline{a} + \overline{b}|^2 =|\overline{a}|^2 + |\overline{b}|^2 + 2\overline{a}\overline{b}\).

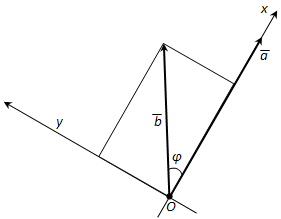
Отсюда видно, что скалярное произведение \(\overline{a}\overline{b}\) выражается через длины векторов \(\overline{a}\), \(\overline{b}\) и \(\overline{a + b}\), а поэтому не зависит от выбора системы координат, т.е. скалярное произведение не изменится, если систему координат выбрать специальным образом. Возьмëм систему координат xy так, как показано на рисунке 225. При таком выборе системы координат координатами вектора \(\overline{a}\) будут \(|\overline{a}|\) и 0, а координатами вектора \(\overline{b}\) будут \(|\overline{a}|\cos\phi\) и \(|\overline{b}|\sin \phi\). Скалярное произведение

\(\overline{a}\overline{b} = |\overline{a}| |\overline{b}|\cos \phi + 0 |\overline{b}| \sin \phi = |\overline{a}| |\overline{b}| \cos \phi\).

Теорема доказана.

Вопрос 26. Докажите, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.
Ответ. Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.