Вопрос 1. Дайте определение косинуса острого угла прямоугольного треугольника.
Ответ. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
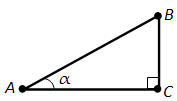
Косинус угла \(\alpha\) обозначается так: \(\cos \alpha\). На рисунке 147 показан прямоугольный треугольник ABC с углом A, равным \(\alpha\). Косинус угла \(\alpha\) равен отношению катета AC, прилежащего к этому углу, к гипотенузе AB, т.е.

\(\cos \alpha = \frac{AC}{AB}\).

Вопрос 2. Докажите, что косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Ответ. Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.
Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.
Доказательство. Пусть ABC и A'B'C' - два прямоугольных треугольника с одним и тем же углом при вершинах A и A', равным \(\alpha\) (рис. 148). Требуется доказать, что

\(\frac{A'C'}{A'B'} = \frac{AC}{AB}\).

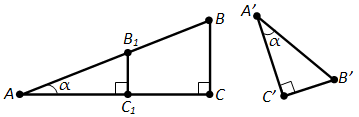
Построим треугольник AB₁C₁, равный треугольнику A'B'C', как показано на рисунке 148. Так прямые BC и B₁C₁ перпендикулярны прямой AC, то они параллельны. По теореме о пропорциональных отрезках

\(\frac{AC₁}{AB₁} = \frac{AC}{AB}\).

А так как по построению AC₁ = A'C', AB₁ = A'B', то

\(\frac{A'C'}{A'B'} = \frac{AC}{AB}\).

Теорема доказана.

Вопрос 3. Докажите теорему Пифагора.
Ответ. Теорема 7.2 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство.Пусть ABC – данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C (рис. 149).

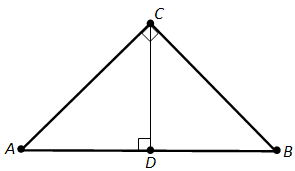
По определению косинуса угла \(\cos A = \frac{AD}{AC} = \frac{AC}{AB}\). Отсюда \(AB \cdot AD = AC^2\). Аналогично \(\cos B = \frac{BD}{BC} = \frac{BC}{AB}\). Отсюда \(AB \cdot BD = BC^2\). Складывая полученные равенства почленно и замечая, что \(AD + DB = AB\), получим:

\(AC^2 + BC^2 = AB (AD + DB) = AB^2\).

Теорема доказана.

Вопрос 4. Докажите, что в прямоугольном треугольнике гипотенуза больше любого из катетов.
Ответ. По теореме 7.2 \(AC^2 + BC^2 = AB^2\). Отсюда, \(AC^2 = AB^2 - BC^2\) и \(BC^2 = AB^2 - AC^2\). Так как величина любого отрезка больше нуля, то \(BC > 0\) и \(AC > 0\). Отсюда, \(AC^2 < AB^2\) и \(BC^2 < AB^2\), т.е. \(AC < AB\) и \(BC < AB\). Так как AC и BC – катеты, а AB – гипотенуза, то из этого следует, что в любом прямоугольном треугольнике гипотенуза больше любого из катетов. Также следует отметить, что в любом прямоугольном треугольнике любой из катетов меньше гипотенузы.

Вопрос 5. Докажите, что \(\cos\alpha<1\) для острого угла \(\alpha\).
Ответ. Если бы в прямоугольном треугольнике гипотенуза была бы равна одному из катетов, то \(\cos\alpha = 1\) (если любое число разделить на это же число, то получим 1). Но это невозможно, так как в любом прямоугольном треугольнике гипотенуза не равна катетам (она больше любого из катетов). Значит, в прямоугольном треугольнике \(\cos\alpha \neq 1\).
Если бы в прямоугольном треугольнике катеты были бы больше гипотенузы, то \(\cos\alpha > 1\) (если большее число разделить на меньшее, то мы получим смешанное число, значение которого больше 1). Но это также невозможно.
Так как в любом прямоугольном треугольнике катеты меньше гипотенузы, то это значит, что \(\cos\alpha < 1\) (если разделить меньшее число на большее, то мы получим обыкновенную дробь, значение которой меньше 1). Значит, в прямоугольном треугольнике для острого угла \(\alpha\) \(\cos\alpha < 1\).

Вопрос 6. Докажите, что если из одной точки к прямой проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра. Равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.
Ответ. Из теоремы Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.
Действительно (см. рис. 152), по теореме Пифагора

\(AB^2 + AC^2 = BC^2\).

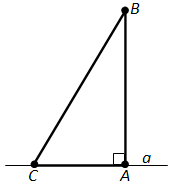
Отсюда, \(AB^2 =BC^2 - AC^2\) и \(BC^2 = AB^2 - AC^2\). Так как величина любого отрезка больше нуля, то \(AB > 0\). Отсюда, \(AB^2 < BC^2\), т.е. \(AB < BC\). Значит, любая наклонная больше перпендикуляра.
Из решения задачи 29 к §3 следует, что если две какие-либо наклонные и перпендикуляры равны, то проекции тоже равны. Значит, равные наклонные имеют равные проекции.
Если AB не будет изменяться, то значение BC будет зависеть от значения AC, т.е. чем больше AC, тем больше BC. Значит, из двух наклонных больше та, у которой проекция больше.

Вопрос 7. Докажите неравенство треугольника.
Ответ. Теорема 7.3 (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Это значит, что каждое из этих расстояний меньше или равно суммы двух других.
Доказательство. Пусть A,B,C – три данные точки. Если две точки из трёх или все три точки совпадают, то утверждение теоремы очевидно.
Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например B. В этом случае AB + BC = AC. Отсюда видно, что каждое из трёх расстояний не больше суммы двух других.

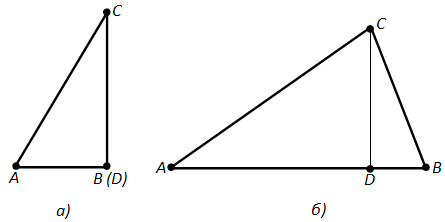
Допустим теперь, что точки не лежат на одной прямой (рис. 154). Докажем, что \(AB < AC + BC\). Опустим перпендикуляр CD на прямую AB. По доказанному \(AB \leq AD + BD\). И так как \(AD < AC\) и \(BD < BC\), то \(AB < AC + BC\). Теорема доказана.

Вопрос 8. Докажите, что в треугольнике каждая сторона меньше суммы двух других сторон.
Ответ. Требуется доказать следующую теорему:
Каков бы ни был треугольник, каждая его сторона меньше суммы двух других сторон.
Доказательство. Пусть ABC –данный треугольник. Как мы знаем, треугольник состоит из точек, не лежащих на одной прямой (рис. 154, б). Докажем, что \(AB < AC + BC\). Опустим перпендикуляр CD на прямую AB. По доказанному \(AB \leq AD + BD\). И так как \(AD < AC\) и \(BD < BC\), то \(AB < AC + BC\). Теорема доказана.

Вопрос 9. Дайте определение синуса и тангенса острого угла. Докажите, что они зависят только от градусной меры угла.
Ответ. Синусом угла \(\alpha\) (обозначается \(\sin \alpha\)) называется отношение противолежащего катета BC к гипотенузе AB:

\(\sin \alpha = \frac{BC}{AB}\).

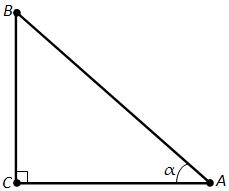
Тангенсом угла \(\alpha\) (обозначается \(tg \alpha\)) называется отношение противолежащего катета BC к прилежащему катету AC:

\(tg \alpha = \frac{BC}{AC}\).

Синус и тангенс угла так же, как и косинус, зависят только от величины угла.
Действительно, по теореме Пифагора

\(BC = \sqrt{AB^2 – AC^2}\).

По определению

\(\sin \alpha = \frac{BC}{AB}\).

Подставим значение BC:

\(\sin \alpha = \frac{\sqrt{AB^2 – AC^2}}{AB} = \sqrt{1 – (\frac{AC}{AB})^2} = \sqrt{1 - \cos^2 \alpha}\).

Так как \(\cos \alpha\) зависит только от величины угла, то и \(\sin \alpha\) зависит только от величины угла.
По определению

\(tg \alpha = \frac{BC}{AC}\).

Разделим числитель и знаменатель на AB:

\(tg \alpha = \frac{BC}{AB} : \frac{AC}{AB} = \frac{sin \alpha}{cos \alpha}\).

Отсюда видно, что и \(tg \alpha\) зависит только от величины угла.

Вопрос 10. Как выражается катет прямоугольного треугольника через гипотенузу и острый угол, через острый угол и другой катет?
Ответ. Из определения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) получаем следующие правила:
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом:
Катет, противолежащий углу \(\alpha\), равен произведению гипотенузы на \(\sin \alpha\).
Катет, прилежащий углу \(\alpha\), равен произведению гипотенузы на \(\cos \alpha\).
Катет прямоугольного треугольника через острый угол и другой катет выражается следующим образом:
Катет, противолежащий углу \(\alpha\), равен произведению второго катета на \(tg \alpha\).