Вопрос 11. Докажите тождества: \(\sin^2\alpha + \cos^2\alpha = 1\); \(1 + tg^2\alpha = \frac{1}{\cos^2 \alpha}\); \(1 + \frac{1}{tg^2 \alpha} = \frac{1}{\sin^2 \alpha}\).
Ответ. Докажем тождества:
\(\sin^2\alpha + \cos^2\alpha = 1 \), \(1 + tg^2\alpha = \frac{1}{\cos^2 \alpha}\), \(1 + \frac{1}{tg^2 \alpha} = \frac{1}{\sin^2 \alpha}\).
Возьмём любой прямоугольный треугольник ABC с углом при вершине A, равным \(\alpha\) (рис. 159). По теореме Пифагора
\(BC^2 + AC^2 = AB^2\).
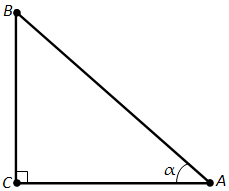
Разделим обе части равенства на \(AB^2\). Получим:
\((\frac{BC}{AB})^2 + (\frac{AC}{AB})^2 = 1\).
Но \(\frac{BC}{AB} = \sin \alpha\), \(\frac{AC}{AB} = \cos \alpha\). Таким образом,
\(\sin^2\alpha + \cos^2\alpha = 1\).
Это равенство есть тождество. Оно верно для любого острого угла \(\alpha\).
Чтобы получить второе тождество, разделим обе части полученного тождества на \(\cos^2 \alpha\). Получим:
\(\frac{\sin^2 \alpha}{cos^2 \alpha} + 1 = \frac{1}{\cos^2 \alpha}\) или \(1 + tg^2 \alpha = \frac{1}{\cos^2 \alpha}\).
Если обе части тождества \(\sin^2 \alpha + \cos^2 \alpha = 1\) разделить на \(\sin^2 \alpha\), то получим третье тождество:
\(1 + \frac{1}{tg^2 \alpha} = \frac{1}{\sin^2 \alpha}\).
Значение этих тождеств заключается в том, что они позволяют, зная одну из величин \(\sin \alpha\), \(\cos \alpha\) или \(tg \alpha\), найти две другие.
Вопрос 12. Докажите, что для любого острого угла \(\alpha\) \(\sin (90° - \alpha ) = \cos \alpha\), \(\cos (90° - \alpha ) = \sin \alpha\).
Ответ. Теорема 7.4. Для любого острого угла \(\alpha\)
\(\sin (90° - \alpha) = \cos \alpha\), \(\cos (90° - \alpha) = \sin \alpha\).
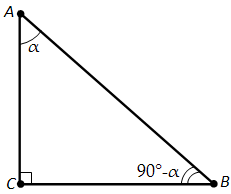
Доказательство. Пусть ABC – прямоугольный треугольник с острым углом \(\alpha\) при вершине A (рис. 160). Тогда острый угол при вершине B равен 90° - \(\alpha\). По определению
\(\sin \alpha = \frac{BC}{AB}\), \(\cos \alpha = \frac{AC}{AB}\),
\(\sin (90° - \alpha) = \frac{AC}{AB}\), \(\cos (90° - \alpha) = \frac{BC}{AB}\).
Из второго и третьего равенств получаем \(\sin (90° - \alpha) = \cos \alpha\). Из первого и четвёртого равенств получаем \(\cos (90° - \alpha) = \sin \alpha\). Теорема доказана.
Вопрос 13. Чему равны значения синуса, косинуса и тангенса углов 30°, 45°, 60°?
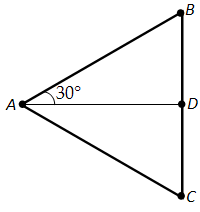
Ответ. Найдём синус, косинус и тангенс угла 30°. Возьмём равносторонний треугольник ABC (рис. 162). Проведём в нём медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине A, равным 30°. Пусть a – сторона равностороннего треугольника. Тогда \(BD = \frac{a}{2}\). По теореме Пифагора
\(AD = \sqrt{AB^2 – BD^2} = \sqrt{a^2 – (\frac{a}{2})^2} = \frac{a\sqrt{3}}{2}\).
Значит,
\(\sin 30° = \frac{a}{2} : a = \frac{a}{2} \cdot \frac{1}{a} = \frac{a \cdot 1}{2 \cdot a} = \frac{1 \cdot 1}{2 \cdot 1} = \frac{1}{2}\); \(\cos 30° = \frac{a\sqrt{3}}{2} : a = \frac{a\sqrt{3}}{2} \cdot \frac{1}{a} = \frac{a\sqrt{3}}{2 \cdot a} = \frac{\sqrt{3}}{2}\);
\(tg 30° = \frac{\sin 30°}{\cos 30°} = \frac{1}{2} : \frac{\sqrt{3}}{2} = \frac{1}{2} \cdot \frac{2}{\sqrt{3}} = \frac{1 \cdot 2}{2 \cdot \sqrt{3}} = \frac{1 \cdot 1}{1 \cdot \sqrt{3}} = \frac{1}{\sqrt{3} = \frac{\sqrt{3}}{3}}\).
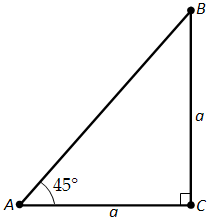
Найдём синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны a. По теореме Пифагора гипотенуза будет \(a \sqrt{2}\). Находим:
\(\sin 45° = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\);
\(\cos 45° = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\); tg 45° = \frac{a}{a} = 1.
Найдём синус, косинус и тангенс угла 60°. Так как \(\sin \alpha = \cos (90° - \alpha)\), то
\(\sin 60° = \cos 30° = \frac{\sqrt{3}}{2}\); \(\cos 60° = \sin 30° = \frac{1}{2}\);
\(tg 60° = \frac{\sin 60°}{\cos 60°} = \sqrt{3}\).
Вопрос 14. Докажите, что \(\sin \alpha\) и \(tg \alpha\) возрастают при возрастании острого угла \(\alpha\), а \(\cos \alpha\) убывает.
Ответ. Теорема 7.5. При возрастании острого угла \(\sin \alpha\) и \(tg \alpha\) возрастают, а \(\cos \alpha\) убывает.
Доказательство. Пусть \(\alpha\) и \(\beta\) – острые углы, причём \(\alpha < \beta\). Отложим углы \(\alpha\) и \(\beta\) от полупрямой AB в одну полуплоскость (рис. 163). Проведём через точку B прямую, перпендикулярную AB. Она пересекает стороны наших углов в точках C и D.
Так как \(\alpha < \beta\), то точка C лежит между точками B и D. Поэтому \(BC < BD\). А значит, по свойству наклонных, проведённых из одной точки к прямой, \(AC < AD\).
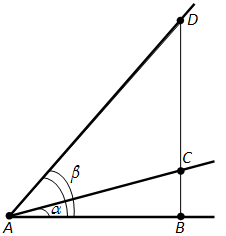
Так как \(\cos \alpha = \frac{AB}{AC}\), \(\cos \beta = \frac{AB}{AD}\), то \(\cos \alpha > \cos \beta\), т.е. при возрастании угла косинус убывает.
Так как \(\sin \alpha = \sqrt{1- \cos^2 \alpha}\), а \(\cos \alpha\) убывает при возрастании угла, то \(\sin \alpha\) возрастает.
Так как \(tg \alpha = \frac{\sin \alpha}{cos \alpha}\) и \(\sin \alpha\) возрастает, а \(\cos \alpha\) убывает при возрастании \(\alpha\), то \(tg \alpha\) возрастает при возрастании \(\alpha\). Теорема доказана.
