Вопрос 1. Объясните, как определяются координаты точки.
Ответ. Проведём на плоскости через точку O две взаимно перпендикулярные прямые x и y – оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось y – осью ординат. Точкой пересечения O – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую – отрицательной.

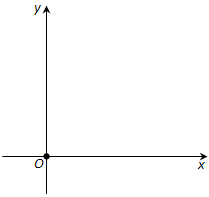
Каждой точке A плоскости мы сопоставим пару чисел – координаты точки – абсциссу (x) и ординату (y) по такому правилу.
Через точку A проведём прямую, параллельную оси ординат (рис. 171). Она пересечёт ось абсцисс x в некоторой точке A_x. Абсциссой точки A мы будем называть число x, абсолютная величина которого равна расстоянию от точки O до точки A_x. Это число будет положительным, если Ax принадлежит положительной полуоси и отрицательным, если A_xпринадлежит отрицательной полуоси. Если точка A лежит на оси ординат y, то полагаем x равным нулю.

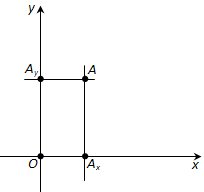
Ордината (y) точки A определяется аналогично. Через точку A проведём прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечёт ось ординат y в некоторой точке A_y. Ординатой точки A мы будем называть число y, абсолютная величина которого равна расстоянию от точки O до точки A_y. Это число будет положительным, если A_y принадлежит положительной полуоси и отрицательным, если A_y принадлежит отрицательной полуоси. Если точка A лежит на оси абсцисс x, то полагаем y равным нулю.
Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: A (x; y) (на первом месте абсцисса, на втором – ордината).

Вопрос 2. Какие знаки у координат точки, если она принадлежит первой (второй, третьей, четвёртой) четверти?
Ответ. Оси координат разбивают плоскость на четыре части – четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения.

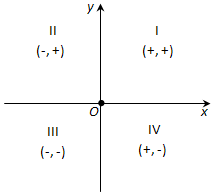
Если точка принадлежит первой четверти, то её абсцисса и ордината будут положительными.
Если точка принадлежит второй четверти, то её абсцисса будет отрицательной, а ордината будет положительной.
Если точка принадлежит третьей четверти, то её абсцисса и ордината будут отрицательными.
Если точка принадлежит четвёртой четверти, то её абсцисса будет положительной, а ордината будет отрицательной.

Вопрос 3. Чему равны абсциссы точек, лежащих на оси ординат?
Чему равны ординаты точек, лежащих на оси абсцисс?
Чему равны координаты начала координат?
Ответ. Точки оси x (оси абсцисс) имеют равные нулю ординаты (y = 0), а точки оси y (оси ординат) имеют равные нулю абсциссы (x = 0).
Если какая-либо точка лежит на оси ординат y, то абсцисса данной точки равна нулю.
Если какая-либо точка лежит на оси абсцисс x, то ордината данной точки равна нулю.
У начала координат абсцисса и ордината равны нулю.

Вопрос 4. Выведите формулы для координат середины отрезка.
Ответ. Пусть A (x₁; y₁) и B (x₂;y₂) – две произвольные точки и C (x; y) – середина отрезка AB. Найдём координаты x, y точки C.
Рассмотрим сначала случай, когда отрезок AB не параллелен оси y, т.е. \(x_1 \neq x_2\). Проведём через точки A, B, C прямые, параллельные оси y (рис. 173). Они пересекут ось x в точках A1 (\(x_1\); 0), B1 (\(x_2\); 0), C (\(x\); 0). По теореме Фалеса точка \(C_1\) будет серединой отрезка \(A_1B_1\).

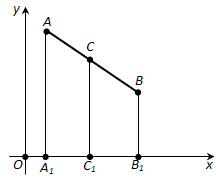
Так как точка \(C_1\) – середина отрезка \(A_1B_1\), то \(A_1C_1 = B_1C_1\), а значит, \(|x – x_1| = |x – x_2|\). Отсюда следует, что либо \(x – x_1 = -(x – x_2)\). Первое равенство невозможно, так как \(x_1 \neq x_2\). Поэтому верно второе. А из него получается формула

\(x = \frac{x_1 + x_2}{2}\).

Если \(x_1 = x_2\), т.е. отрезок AB параллелен оси y, то все три точки \(A_1, B_1, C_1\) имеют одну и ту же абсциссу. Значит, формула остаётся верной и в этом случае.
Ордината точки C находится аналогично. Через точки A, B, C проводятся прямые, параллельные оси x. Получается формула

\(x = \frac{y_1 + y_2}{2}\).

Вопрос 5. Выведите формулу для расстояния между точками.
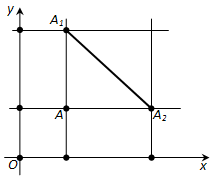
Ответ. Пусть на плоскости xy даны две точки: \(A_1\) с координатами \(x_1, y_1\) и \(A_2\) с координатами \(x_2, y_2\). Выразим расстояние между точками \(A_2\) и \(A_2\) через координаты этих точек.
Рассмотрим сначала случай, когда \(x_1 \neq x_2\) и \(y_1 \neq y_2\). Проведём через точки \(A_1\) и \(A_2\) прямые, параллельные осям координат, и обозначим через A точку их пересечения (рис. 174). Расстояние между точками \(A\) и \(A_1\) равно \(|y_1 – y_2|\), а расстояние между точками \(A\) и \(A_2\) равно \(|x_1 – x_2|\). Применяя к прямоугольному треугольнику \(AA_1A_2\) теорему Пифагора, получим:

\(d^2 = (x_1 - x_2)^2+ (y_1 - y_2)^2\), (*)

где d –расстояние между точками \(A_1\) и \(A\).

Хотя формула (*) для расстояния между точками выведена нами в предположении \(x_1 \neq x_2\), \(y_1 \neq y_2\), она остаётся верной и в других случаях. Действительно, если \(x_1 = x_2\), \(y_1 \neq y_2\), то d равно \(|y_2 - y_2|\). Тот же результат даёт и формула (*). Аналогично рассматривается случай, когда \(x_1 \neq x_2, y_1 = y_2\). При \(x_1 = x_2, y_1 = y_2\) точки \(A_1\) и \(A_2\) совпадают и формула (*) даёт d = 0.

Вопрос 6. Что такое уравнение фигуры в декартовых координатах?
Ответ. Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными x и y, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.

Вопрос 7. Выведите уравнение окружности.
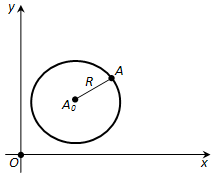
Ответ. Составим уравнение окружности с центром в точке A_O (a; b) и радиусом R (рис. 175). Возьмём произвольную точку A (x; y) на окружности. Расстояние от неё до центра A_O равен \((x – a)^2 + (y – b)^2\). Таким образом, координаты x, y каждой точки A окружности удовлетворяют уравнению

\((x – a)^2 + (y – b)^2 = R^2\). (*)

Обратно: любая точка A, координаты которой удовлетворяют уравнению (*), принадлежит окружности, так как расстояние от неё до точки A_O равно R. Отсюда следует, что уравнение (*) действительно является уравнением окружности с центром A_Oи радиусом R. Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:

\(x^2 + y^2 = R^2\).

Вопрос 8. Докажите, что прямая в декартовых координатах имеет уравнение вида ax + by + c = 0.
Ответ. Докажем, что любая прямая в декартовых координатах x, y имеет уравнение вида

ax + by + c = 0, (*)

где a, b, c – некоторые числа.
Пусть h – произвольная прямая на плоскости xy. Проведём какую-нибудь прямую, перпендикулярную прямой h, и отложим на ней от точки пересечения C с прямой h равные отрезки CA₁ и CA₂(рис. 176).

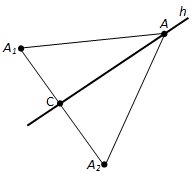
Пусть a₁, b₁ – координаты точки A₁ и a₂, b₂ – координаты точки A₂. Как мы знаем, любая точка A (x; y) прямой h равноудалена от точек A₁ и A₂. Поэтому координаты её удовлетворяют уравнению

\((x – a_1)^2 + (y - b_1)^2 = (x – a_2)^2 + (y - b_2)^2\). (**)

Обратно: если координаты x и y какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек A₁ и A₂, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:

\(2(a_2 - a_1)x + 2(b_2 - b_1)y + (a_1^2 + b^2_1 - a^2_2 - b^2_2) = 0.\)

Обозначая \(2(a_2 - a_1) = a\), \(2(b_2 - b_1) = b\), \(a^2_1 + b^2_1 - a^2_2 - b^2_2 = c\), получаем уравнение (*). Утверждение доказано.

Вопрос 9. Как найти координаты точки пересечения двух прямых, если заданы уравнения этих прямых?
Ответ. Пусть заданы уравнения двух прямых:

ax + by + c = 0,

a₁x + b₁y + c₁ = 0.

Найдём координаты их точки пересечения.
Так как точка пересечения (x; y) принадлежит каждой из прямых, то её координаты удовлетворяют и первому и второму уравнению. Поэтому координаты точки пересечения являются решением системы уравнений, задающих прямые. Рассмотрим пример.
Пусть уравнениями данных прямых будут:

3x – y + 2 = 0,

5x – 2y + 1 = 0.

Решая эту систему уравнений, находим x = -3, y = -7. Точка пересечения прямых (-3; -7).

Вопрос 10. Как расположена прямая, если в её уравнении коэффициент a = 0 (b = 0; c = 0)?
Ответ. Выясним, как расположена прямая относительно осей координат, если её уравнение ax + by + c = 0 имеет тот или иной частный вид.
1. a = 0, b \(\neq\) 0. В этом случае уравнение прямой можно переписать так:

\(y = -\frac{c}{b}\).

Таким образом, все точки прямой имеют одну и ту же ординату (\(-\frac{c}{b}\)); следовательно, прямая параллельна оси x (рис. 177, а). В частности, если c = 0, то прямая совпадает с осью x.
2. b = 0, a \(\neq\) 0. Этот случай рассматривается аналогично. Прямая параллельна оси y (рис. 177, б) и совпадает с ней, если c = 0.

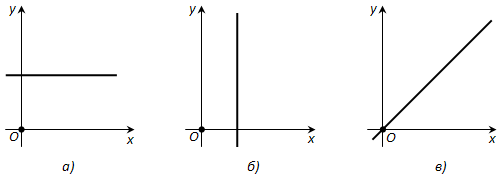
3. c = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 177, в).

Вопрос 11. Что такое угловой коэффициент прямой и какой его геометрический смысл?
Ответ. Если в общем уравнении прямой ax + by + c = 0 коэффициент при y не равен нулю, то это уравнение можно разрешить относительно y. Получим:

\(y = -\frac{a}{b}x - \frac{c}{b}\).

Или, обозначая \(-\frac{a}{b} = k\), \(-\frac{c}{b} = l\), получим:

y = kx + l.

Выясним геометрический смысл коэффициента k в этом уравнении.
Возьмём две точки на прямой A (x₁; y₁), B(x₂; y₂) (x₁ < x₂). Их координаты удовлетворяют уравнению прямой:

y₁ = kx₁ + l, y₂ = kx₂ + l.

Вычитая эти равенства почленно, получим y₂ - y₁ = k (x₂ - x₁). Отсюда

\(k = \frac{y_2 - y_1}{x_2 - x_1}\).

В случае, представленном на рисунке 178, а, \(\frac{y_2 - y_1}{x_2 - x_1} = tg \alpha\).
В случае, представленном на рисунке 178, б, \(\frac{y_2 - y_1}{x_2 - x_1} = -tg \alpha\).

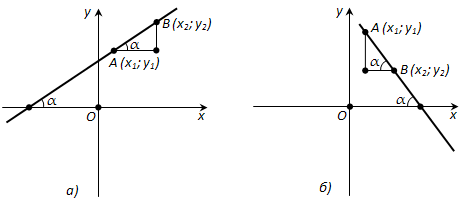
Таким образом, коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x. Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.

Вопрос 12. Докажите, что графиком линейной функции является прямая.
Ответ. Пусть y = ax + b - данная линейная функция. Докажем, что еë графиком является прямая.
Для данной функции если x = 0, то y = b, если x = 1, то y = a + b. Поэтому графику функции принадлежат точки (0; b) и (1; a + b). Составим уравнение прямой, проходящей через эти точки. Как мы знаем, оно имеет вид:

y = kx + l.

Так как указанные точки графика лежат на прямой, то их координаты удовлетворяют уравнению прямой:

\(b = k \cdot 0 + l\),

\(a + b = k \cdot 1 + l\).

Отсюда находим l = b, k = a. Итак, наша прямая имеет уравнение

y = ax + b.

Значит, уравнению прямой удовлетворяют все точки графика. То есть графиком линейной функции является прямая.

Вопрос 13. При каком условии прямая и окружность не пересекаются, пересекаются в двух точках, касаются?
Ответ. Пусть R – радиус окружности и d – расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось x (рис. 179). Тогда уравнением окружности будет \(x^2 + y^2 = R^2\), а уравнением прямой x = d.
Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений

\(x^2 + y^2 = R^2\), x = d

имела решение. И обратно: всякое решение этой системы даёт координаты x, y точки пересечения прямой с окружностью. Решая нашу систему, получим:

x = d, \(y = \pm\sqrt{R^2 – d^2}\).

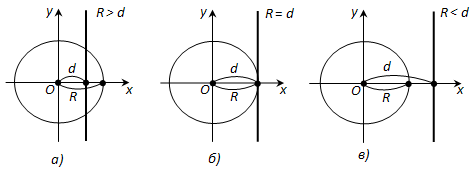
Из выражения для y видно, что система имеет два решения, т.е. окружность и прямая имеют две точки пересечения, если R > d (рис. 179, а).
Система имеет одно решение, если R = d (рис. 179, б). В этом случае прямая и окружность касаются.
Система не имеет решения, т.е. прямая и окружность не пересекаются, если R < d (рис. 179, в).

Вопрос 14. Дайте определение синуса, косинуса и тангенса для любого угла от 0° до 180°.
Ответ. Возьмём окружность на плоскости xy с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси x в верхнюю полуплоскость (полуплоскость, где y > 0) угол \(\alpha\). Пусть x и y – координаты точки A. Значения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) для острого угла \(\alpha\) выражаются через координаты точки A, а именно:

\(\cos \alpha = \frac{x}{R}\), \(\sin \alpha = \frac{y}{R}\), \(tg \alpha = \frac{y}{x}\).

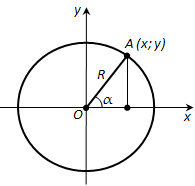
Определим теперь значения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) этими формулами для любого угла \(\alpha\). (Для \(tg \alpha\) угол \(\alpha = 90°\) исключается.)
При таком определении \(\sin 90° = 1\), \(\cos 90° = 0\), \(\sin 180° = 0\), \(\cos 180° = -1\), \(tg 180° = 0\).
Считая, что совпадающие лучи образуют угол 0°, будем иметь: \(\sin 0° = 0\), \(\cos 0° = 1\), \(tg 0° = 0\).

Вопрос 15. Докажите, что для любого угла \(\alpha\), \(0° < \alpha < 180°\),
\(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\),
\(tg (180° - \alpha) = -tg \alpha\).
Ответ. Докажем, что для любого угла \(\alpha\), \(0° < \alpha < 180°\), \(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\). Для угла \(\alpha \neq 90°\) \(tg (180° - \alpha) = -tg \alpha\).

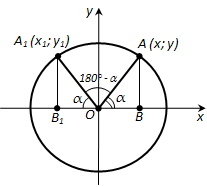
Действительно, треугольники OAB и OA₁>B₁ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что AB = A₁B₁, т.е. y = y₁; OB = OB₁, следовательно, x = -x₁. Поэтому

\(\sin (180° - \alpha) = \frac{y_1}{R} = \frac{y}{R} = \sin \alpha\),

\(\cos (180° - \alpha) = \frac{x_1}{R} = \frac{-x}{R} = -\cos \alpha\).

Разделив почленно равенство \(\sin (180° - \alpha) = \sin \alpha\) на равенство \(\cos (180° - \alpha) = -\cos \alpha\), получаем:

\(tg (180° - \alpha) = -tg \alpha\).

Что и требовалось доказать.