Вопрос 11. Что такое угловой коэффициент прямой и какой его геометрический смысл?
Ответ. Если в общем уравнении прямой ax + by + c = 0 коэффициент при y не равен нулю, то это уравнение можно разрешить относительно y. Получим:

\(y = -\frac{a}{b}x - \frac{c}{b}\).

Или, обозначая \(-\frac{a}{b} = k\), \(-\frac{c}{b} = l\), получим:

y = kx + l.

Выясним геометрический смысл коэффициента k в этом уравнении.
Возьмём две точки на прямой A (x₁; y₁), B(x₂; y₂) (x₁ < x₂). Их координаты удовлетворяют уравнению прямой:

y₁ = kx₁ + l, y₂ = kx₂ + l.

Вычитая эти равенства почленно, получим y₂ - y₁ = k (x₂ - x₁). Отсюда

\(k = \frac{y_2 - y_1}{x_2 - x_1}\).

В случае, представленном на рисунке 178, а, \(\frac{y_2 - y_1}{x_2 - x_1} = tg \alpha\).
В случае, представленном на рисунке 178, б, \(\frac{y_2 - y_1}{x_2 - x_1} = -tg \alpha\).

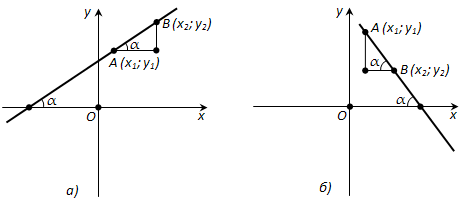
Таким образом, коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x. Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.

Вопрос 12. Докажите, что графиком линейной функции является прямая.
Ответ. Пусть y = ax + b - данная линейная функция. Докажем, что еë графиком является прямая.
Для данной функции если x = 0, то y = b, если x = 1, то y = a + b. Поэтому графику функции принадлежат точки (0; b) и (1; a + b). Составим уравнение прямой, проходящей через эти точки. Как мы знаем, оно имеет вид:

y = kx + l.

Так как указанные точки графика лежат на прямой, то их координаты удовлетворяют уравнению прямой:

\(b = k \cdot 0 + l\),

\(a + b = k \cdot 1 + l\).

Отсюда находим l = b, k = a. Итак, наша прямая имеет уравнение

y = ax + b.

Значит, уравнению прямой удовлетворяют все точки графика. То есть графиком линейной функции является прямая.

Вопрос 13. При каком условии прямая и окружность не пересекаются, пересекаются в двух точках, касаются?
Ответ. Пусть R – радиус окружности и d – расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось x (рис. 179). Тогда уравнением окружности будет \(x^2 + y^2 = R^2\), а уравнением прямой x = d.
Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений

\(x^2 + y^2 = R^2\), x = d

имела решение. И обратно: всякое решение этой системы даёт координаты x, y точки пересечения прямой с окружностью. Решая нашу систему, получим:

x = d, \(y = \pm\sqrt{R^2 – d^2}\).

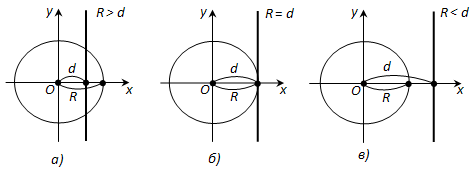
Из выражения для y видно, что система имеет два решения, т.е. окружность и прямая имеют две точки пересечения, если R > d (рис. 179, а).
Система имеет одно решение, если R = d (рис. 179, б). В этом случае прямая и окружность касаются.
Система не имеет решения, т.е. прямая и окружность не пересекаются, если R < d (рис. 179, в).

Вопрос 14. Дайте определение синуса, косинуса и тангенса для любого угла от 0° до 180°.
Ответ. Возьмём окружность на плоскости xy с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси x в верхнюю полуплоскость (полуплоскость, где y > 0) угол \(\alpha\). Пусть x и y – координаты точки A. Значения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) для острого угла \(\alpha\) выражаются через координаты точки A, а именно:

\(\cos \alpha = \frac{x}{R}\), \(\sin \alpha = \frac{y}{R}\), \(tg \alpha = \frac{y}{x}\).

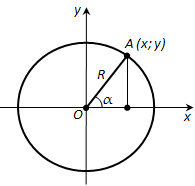
Определим теперь значения \(\sin \alpha\), \(\cos \alpha\) и \(tg \alpha\) этими формулами для любого угла \(\alpha\). (Для \(tg \alpha\) угол \(\alpha = 90°\) исключается.)
При таком определении \(\sin 90° = 1\), \(\cos 90° = 0\), \(\sin 180° = 0\), \(\cos 180° = -1\), \(tg 180° = 0\).
Считая, что совпадающие лучи образуют угол 0°, будем иметь: \(\sin 0° = 0\), \(\cos 0° = 1\), \(tg 0° = 0\).

Вопрос 15. Докажите, что для любого угла \(\alpha\), \(0° < \alpha < 180°\),
\(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\),
\(tg (180° - \alpha) = -tg \alpha\).
Ответ. Докажем, что для любого угла \(\alpha\), \(0° < \alpha < 180°\), \(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\). Для угла \(\alpha \neq 90°\) \(tg (180° - \alpha) = -tg \alpha\).

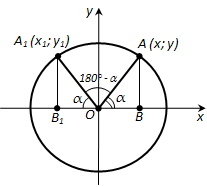
Действительно, треугольники OAB и OA₁>B₁ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что AB = A₁B₁, т.е. y = y₁; OB = OB₁, следовательно, x = -x₁. Поэтому

\(\sin (180° - \alpha) = \frac{y_1}{R} = \frac{y}{R} = \sin \alpha\),

\(\cos (180° - \alpha) = \frac{x_1}{R} = \frac{-x}{R} = -\cos \alpha\).

Разделив почленно равенство \(\sin (180° - \alpha) = \sin \alpha\) на равенство \(\cos (180° - \alpha) = -\cos \alpha\), получаем:

\(tg (180° - \alpha) = -tg \alpha\).

Что и требовалось доказать.